Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 16
- Elimine o parâmetro para encontrar uma equação cartesiana da curva.
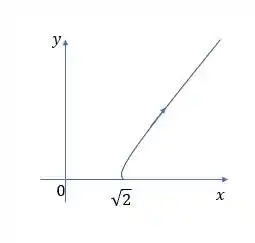
- Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta.
Passo 1
Olá, meu querido e nobre estudante. Vamos resolver mais uma atividade juntos aqui.
A gente tem a curva parametrizada:
E vamos fazer duas coisas, vamos primeiro passar essa equação para as coordenadas cartesianas. E também vamos criar o esboço do gráfico.
Para colocarmos em coordenadas cartesianas, precisamos isolar o em uma das duas equações e substituirmos na outra equação.
Já para o esboço do gráfico, a gente vai criar uma tabela, iremos colocar diversos valores de e seus respectivos e .
Passo 2
Letra a)
Temos que então que:
Vamos elevar ao quadrado ambas as equações:
E
Agora vamos isolar o :
E
Igualando o :
Dividindo a equação por :
Recorde-se do seu conhecimento sobre cônicas que esta é uma hipérbole centrada na origem com um eixo transversal horizontal. Mas, devido às restrições de domínio, apenas a porção do quadrante dela.
Passo 3
Letra b)
Vamos então ao gráfico. Vamos criar uma tabela com diversos valores para e seus respectivos valores e e :
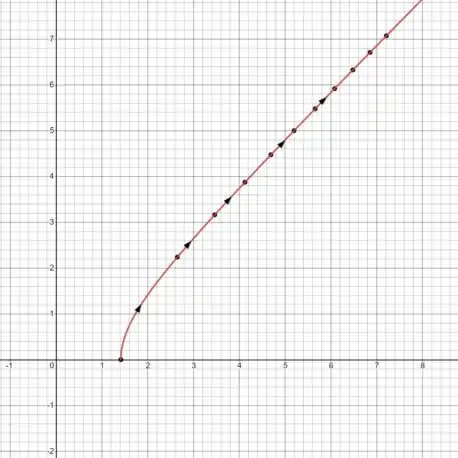
Agora vamos plotar esses pontos no GeoGebra, e assim iremos construir o esboço da nossa curva:
Veja que conforme aumenta, o ponto se move na direção para cima/direita.
Resposta
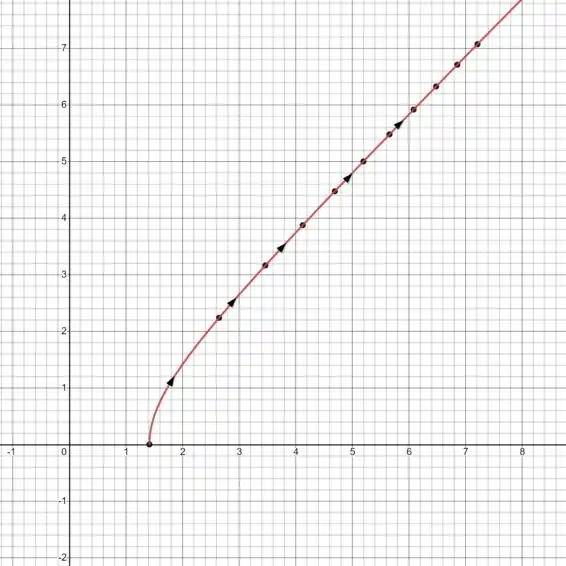
Resposta
