Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.3 - Ex. 36
Empregue o Teorema do Confronto para mostrar que
Ilustre, fazendo os gráficos, na mesma tela, das funções , e (como no Teorema do Confronto).
Passo 1
Eaee, belezinha?? Bom... queremos demonstrar o seguinte limite utilizando o Teorema do Confronto:
Bom... o teorema do confronto é bem interessante pra quando temos funções como seno e cosseno porque elas são limitadas. Você vai ver!
O Teorema do Confronto diz que se uma função está limitada por outras 2 funções, uma maior e uma menor:
Se o limite das duas funções for igual num ponto
Então o limite de também vai ser igual nesse ponto
Interessante ne? Assim, caso a gente não consiga calcular o limite de , a gente pode encontrar seu valor a partir do limite das outras duas funções!
Então nosso primeiro passo é definir essas 3 funções que se relacionam assim:
E o seno vai nos ajudar nisso!
Passo 2
Vamos lá, temos a função seno na nossa expressão, podemos começar dizendo que a função seno se limita entre os valores , assim:
Agora vamos multiplicar tudo por , deixando a função igual a do limite:
Assim temos as funções
Agora nós temos uma das condição do Teorema do Confronto:
Vamos agora testar a próxima condição, se:
Passo 3
Vemos que
e que
Opa, são iguais!
Então, pelo Teorema do Confronto, podemos concluir que o limite da nossa também vai ser igual::
Passo 4
E aqui temos o plot dos gráficos:
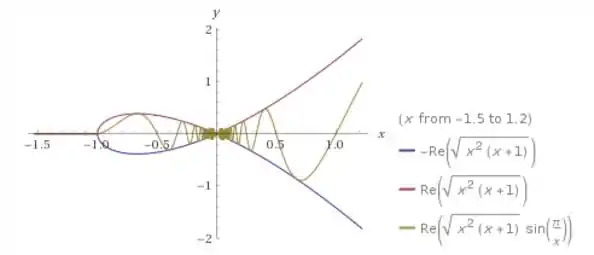
Nossa função é a curva amarela. Ela está limitada pelas outras 2 em todo seu domínio. Então no ponto em qua as curvas rosa e roxa tem o mesmo limite, o limite das 3 tem que ser igual, pra que continue limitada.
Resposta
Demonstração