Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.3 - Ex. 35
Use o Teorema do Confronto para mostrar que
Ilustre, fazendo os gráficos das funções , e na mesma tela.
Passo 1
Eaee, belezinha?? Bom... queremos demonstrar o seguinte limite utilizando o Teorema do Confronto:
Bom... o teorema do confronto diz que:
Sejam , funções reais definidas no dominio e seja a um ponto dentro desse dominio, se:
E
Então
No nosso caso vamos usar que a função cosseno está entre e
Assim multiplicando tudo por conseguiremos calcular o limite da nossa função, afinal sabemos os seguintes limites:
Agora vamos aplicar!!
Passo 2
Vamos lá, temos a função cosseno na nossa expressão, podemos começar dizendo que a função cosseno se limita entre os valores , assim:
Agora vamos multiplicar tudo por , deixando a função igual a do limite:
Agora nós temos uma das condição do Teorema do Confronto:
Vamos agora testar a próxima condição, se:
Passo 3
Vemos que
e que
Assim,
Então, pelo Teorema do Confronto podemos concluir que:
E aqui temos o plot dos gráficos:
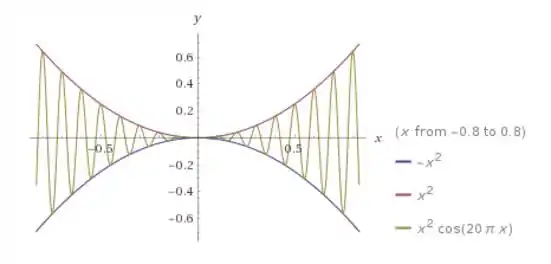
Onde temos a função em vermelho em cima, a função em azul embaixo e a função de interesse no meio. Vemos então o teorema do confronto acontecendo e que quando tende a zero, a função de cima e a de baixo tendem a zero. Portanto, a função do meio que é a que queremos calcular o limite também tende a zero.
Resposta
Demonstração