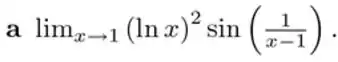Exercícios de Teorema do Confronto - Lista de Exercícios Resolvida

Use as propriedades de limite para calcular

Considere uma função satisfazendo

Para todo . Calcule, para essa função,

Calcule o limite, se possível. Caso conclua que o limite não existe, justifique.

Resolva o limite:

Calcule o limite:

Calcule o limite, caso exista. Caso não exista, justifique.

Calcule o limite ou explique porque não existe.

Calcule, caso existam, os seguintes limites:

18) Sabendo que para , satisfaz , calcule .

Use o Teorema do Confronto para mostrar que

Seja uma função tal que , para . Calcule .

Seja uma função tal que , para todo . Calcule .

Seja uma função satisfazendo a propriedade

para todo x>0. Calcule

Calcule o limite ou prove que não existe:

Calcule o limite ou prove que não existe:

Considere uma função satisfazendo

Para todo . Calcule, para essa função,

Calcule o limite

Seja uma função limitada. Use o teorema do Anulamento (é o corolário do teorema do confronto) para provar que .

Calcule o limite, caso exista. Caso não exista, justifique.

2. Seja uma função que satisfaz

Calcule o seguinte limite:

Calcule os seguintes limites

(b)

9. Existe um número tal que exista? Caso exista, encontre e o valor do limite.

Calcule os limites abaixo. Justifique suas respostas.

d)

Calcule os seguintes limites:

Q01c) Avalie os limites abaixo e encontre o correspondente valor caso exista. Justifique suas respostas:

1. Calcule, se existirem, os limites abaixo.

Calcule o limite ou justifique porque não existe:

O movimento de uma mola sujeita a uma força de atrito é frequentemente modelado pelo produto de uma função exponencial e uma função seno. Suponha que a equação do movimento de um ponto sobre essa mole é:

em que s é medida em centímetros e t em segundos.

Mostre que . Interprete o significado desse limite.

Calcule os limites abaixo. Justifique suas respostas.

1. Calcule, se existirem, os limites abaixo.

2c) Calcule os limites abaixo ou prove que não existe (sem usar a Regra de L'Hospital).

Sem usar a regra de L’Hospital, calcule o limite ou prove que não existe:

Calcule o limite, caso exista. Caso não exista, justifique.

13. Demonstre que

Seja tal que , para todo . Mostre que e use-o para determinar

16) Calcule cada limite, quando possível. Caso conclua que o limite não existe, justifique.

Considere as funções dadas por

E

1. Verifique se é contínua em
2. Verifique se é diferenciável em . Se sim, quanto vale ?

3. Calcule os seguintes limites (Não pode usar a regra de ):

a)

3. Calcule os seguintes limites (Não pode usar a regra de ):

b)

17) Seja uma função limitada. Use o teorema do anulamento (é o corolário do teorema do confronto) para provar que .

16)A função é tal que para , satisfaz . Calcule .

26) Calcule o limite, caso exista. Caso não exista, justifique.

16) Calcule cada limite, quando possível. Caso conclua que o limite não existe, justifique.

15) Calcule cada limite, quando possível. Caso conclua que o limite não existe, justifique.

1) Encontre, caso existam, os limites abaixo:

c)

13. Demonstre que

2. Seja uma função que satisfaz para todo . Calcule

Verifique que, se , para todo , então é contínua em . O que se pode afirmar sobre a continuidade em .

Calcule o limite, se possível. Caso conclua que não existe, justifique.

Calcule o limite, caso exista. Caso não exista, justifique.

O movimento de uma mola sujeita a uma força de atrito é frequentemente modelado pelo produto de uma função exponencial e uma função seno. Suponha que a equação do movimento de um ponto sobre essa mole é:

em que s é medida em centímetros e t em segundos.

Mostre que . Interprete o significado desse limite.

1. Seja uma função definida em tal que

Calcule e justifique.

2. Seja uma função definida em tal que , para todo . Calcule e justifique.

3. Suponha que , para todo . Calcule .

Calcule .

Seja uma função definida em ℝ e suponha que exista uma constante tal que

,

para todo .

Calcule, caso exista,

5. Usando um Corolário do Teorema do Confronto, mostre que a função tem limite no ponto nos seguintes casos:

(b) e

Sugestão: Obtenha uma fatoração do tipo , em que é limitada próximo do ponto e

Calcule o limite, se possível. Caso conclua que não existe, justifique.

7 – Calcule cada um dos limites abaixo.

d)

1. Calcule os seguintes limites:

c.

3. Use o Teorema do Confronto para mostrar que . Ilustre fazendo os gráficos, no mesmo sistema de coordenadas, , e .

5. Usando um Corolário do Teorema do Confronto, mostre que a função tem limite no ponto nos seguintes casos:

(a) e

Calcule .

O limite existe?

O limite existe?

Mostre que a equação tem pelo menos uma solução real.

Mostre que a equação tem pelo menos três soluções reais.

Seja . Existe pertencente a tal que ?

Seja contínua, com e para todo . Mostre que para todo .

Mostre que o conjunto

admite um maior e um menor elemento. Você consegue calcular estes valores?

Calcule os limites abaixo:

a)

Calcule os limites abaixo:

b)

Considere a função

Existe ? Em caso afirmativo, determine o seu valor.

Seja uma função satisfazendo para todo . Mostre que

Podemos dizer alguma coisa sobre ?

Calcule o limite ou prove que não existe:

Suponha que, para todo , . Use o Teorema do Confronto para calcular

Mostre que .

Calcule o limite

Se

para , encontre

(NÃO é permitido o uso da Regra de L’Hôpital)

38. Calcule, caso exista , onde é dada por

b)

44. Empregue o Teorema do Confronto para mostrar que

Ilustre, fazendo os gráficos das funções e (como no Teorema do Confronto) na mesma tela.

46. Calcule.

d)

Calcule o limite ou prove que não existe:

2. Seja uma função limitada. Calcule os limites abaixo, se existirem

Avalie os limites abaixo e encontre o correspondente valor caso exista. Justifique suas respostas.

8. Se , encontre

12. Se para , encontre .

Sejam e assuma que para todo . Mostre que

Avalie o limite abaixo e encontre o correspondente valor caso exista.

Demonstre o Teorema da Comparação dado em salsa de aula: Sejam f e g funções tais que para , para algum Se o e existem, então .

Demonstre o Corolário do Teorema do Confronto dado em sala de aula: Suponha e que existam satisfazendo . Então . [Sugestão: Use o Teorema do Confronto e o Exercício 3.]

Calcule, caso exista, os limites abaixo (em alguns casos você pode usar o teorema do confronto).

45. Se para , encontre .