Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.3 - Ex. 3
Marque o ponto cujas coordenadas polares são dadas. A seguir encontre as coordenadas cartesianas no ponto.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu os seguintes pontos dados em coordenadas polares:
Queremos encontrar as coordenadas cartesianas desses pontos.
Para isso, temos que saber que um ponto no plano cartesiano pode ser dado tanto em coordenadas polares quanto cartesianas:
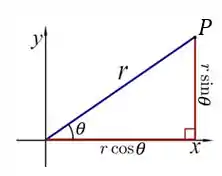
Assim, de acordo com a figura, as coordenadas cartesianas para um ponto dado em coordenadas polares são dadas por:
Agora bora aplicar! 😉
Passo 2
Aplicando os conceitos do Passo 1 para o ponto , temos:
E
Assim, temos a seguinte coordenada cartesiana:
Passo 3
Agora, aplicando os conceitos do Passo 1 para o ponto , temos:
E
Assim, temos a seguinte coordenada cartesiana:
Passo 4
Finalmente, aplicando os conceitos do Passo 1 para o ponto , temos:
E
Assim, temos a seguinte coordenada cartesiana: