Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.3 - Ex. 5

As coordenadas cartesianas de um ponto são dadas.

(i)Encontre as coordenadas polares r , θ . Onde r > 0 e 0 ≤ θ ≤ 2 π .

(ii) Encontre as coordenadas polares r , θ . Onde r < 0 e 0 ≤ θ ≤ 2 π .

  1. ( 2 ,   - 2 )
  2. ( - 1 , 3 )

Passo 1

Olá, meu nobre e querido amigo. Vou te ajudar a resolver essa atividade.

Aqui a gente precisa encontrar as coordenadas polares dos pontos cartesianos:

( 2 ,   - 2 )

( - 1 , 3 )

Isso a gente faz utilizando as relações entre coordenadas polares e cartesianas:

x = r ⋅ cos ⁡ θ   ;   y = r ⋅ s e n θ

Iremos encontrar primeiro o r , que é dado por:

r 2 = x 2 + y 2

E a partir disso iremos substituir nas fórmulas de x e y . Depois de substituirmos nas fórmulas de x e y , poderemos encontrar os valores de θ com ajuda do círculo trigonométrico abaixo:

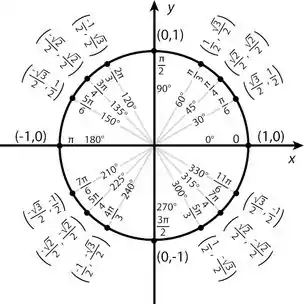
A gente tem os ângulos e o seu c o s s e n o e s e n o

Passo 2

Na letra (a) a coordenada cartesiana é x = 2 ,   y = - 2 .

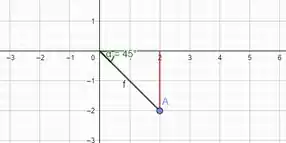
Perceba que colocando os pontos no plano cartesiano e fechando um triângulo como mostra em vermelho, teremos x   e   y como catetos e o raio como hipotenusa. Nesse caso a hipotenusa

h = 2 2 + - 2 2

h = 2 2

e então esse é nosso raio.

Agora é só substituir nas equações seguintes:

x = r ⋅ cos ⁡ θ                                                       y = r ⋅ s e n θ

Chegamos em um ângulo de 45 º = π 4   no quarto quadrante já que o cosseno deu positivo e o seno negativo. Então nossa primeira resposta com o raio positivo seria ( 2 2 , 7 π 4 )

Um outro meio de representar seria deixando o raio negativo e pra isso invertemos o ângulo no quadrante oposto, veja no círculo trigonométrico abaixo o ângulo oposto quando mudamos o sinal de r .

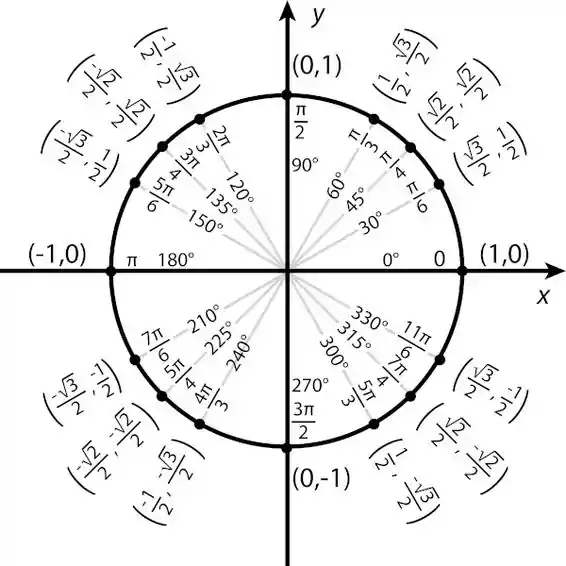
chegando a ( - 2 2 , 3 π 4 ) .

Passo 3

Na letra (b) a coordenada nos diz que x = - 1   e   y = 3 . Aí usando a mesma lógica a hipotenusa, que podemos chamar de raio vai ser 2 . E através das equações:

- 1 2 = cos ⁡ θ   ;   3 2 = s e n θ

Sabemos que o ângulo é de 60 º e para descobrir os quadrantes é só olhar os sinais. Como cosseno é medido no eixo x e ele está negativo da pra ter uma base que o ponto está no 2 º   ou   3 º quadrante.

Agora, se o seno é medido no eixo y e está positivo, chegamos na conclusão que está no 2 º . A coordenada fica   ( 2 ,   4 π 6 ) , que simplificando a fração:

( 2 ,   2 π 3 )

Um outro meio de escrever é colocando o raio negativo, invertendo então os quadrantes. Faríamos então que o ângulo andasse 60 º no sentido horário, ou seja, o mesmo que dizer que o ângulo andou 300 º e jogamos o raio para o outro lado, ficando:

( - 2 , 5 π 3 )

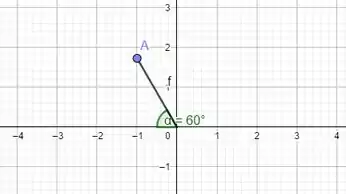
Resposta

  1. 2 2 , 7 π 4 e   ( - 2 2 , 3 π 4 ) .
  2. 2 ,   2 π 3 e   ( - 2 , 5 π 3 ) .    
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

r = 5 3 + 3 s e n θ . (a) ache a excentricidade; (b) identifique a cônica; (c) escreva a equação da diretriz que corresponde ao foco na origem; (d) faça um esboço da curva.
Ache a área da região limitada por um laço da curva r = as e nn θ , onde n é um número inteiro positivo.
Ache a equação polar da circunferência com centro em ( r 0 ,θ 0 ) e raio a unidades.
Ache a equação polar da cônica que satisfaz as condições dadas e faça um esboço do gráfico. A reta rs e n θ = 6 é a diretriz correspondente ao foco na origem e e = 5 3 .
Ache a equação polar da cônica que satisfaz as condições dadas e faça um esboço do gráfico. Um foco na origem; Um vertice em ( 6 ,1 2 π ); e = 1 ;