Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 1.4 - Ex. 14b
Encontrar a curva de interseção do gráfico da função dada com os planos dados, representando graficamente:
(b) com os planos .
Passo 1
Pessoal, para encontrarmos a curva resultante da interseção do gráfico de uma função com um plano, basta substituirmos um no outro! Assim, pro plano , temos:
Essa é a equação de uma circunferência de raio
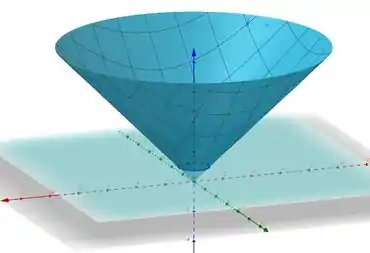
Passo 2
Para o plano :
Aqui, temos a equação de uma função modular!
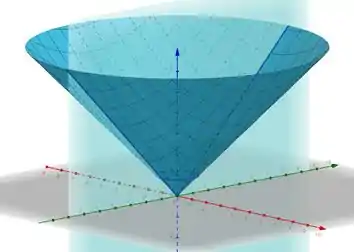
Passo 3
Para o plano , temos:
Nesse caso, temos a equação de uma parábola também!
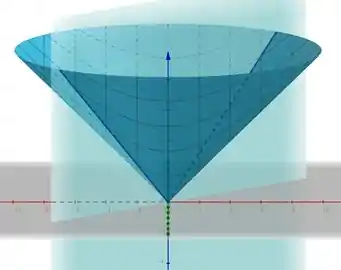
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Desenhar algumas curvas de nível e esboçar o gráfico: z =3 -2 x - 3 y
Desenhar algumas curvas de nível e esboçar o gráfico:(f) z = 9 - x 2 - y 2
Desenhar algumas curvas de nível e esboçar o gráfico:(e) z = y 2 ,- 4 ≤ x ≤ 4 ,0 ≤ y ≤ 2
Desenhar algumas curvas de nível e esboçar o gráfico:(c) z = 3 - 2 x - 3 y
Desenhar algumas curvas de nível e esboçar o gráfico:(g) z = x 2 + y 2 - 2