Se , encontre , , , , , , , , e .

Primeiro queremos encontrar , então temos que substituir onde o aparece por :

Fazendo as continhas:

Ficamos com o resultado:

Bom, aqui é bem parecido com o item anterior, mas no lugar de iremos fazer . Olha só:

Agora é só ajeitar esses sinais negativos e fazer as continhas! Só um lembrete: todo número negativo ao quadrado dá um resultado positivo, beleza? Isso vai ajudar lá agora e lá na frente, então sempre tenha isso em mente! Olha com fica:

O que vai resultar na seguinte expressão final:

Nesse próximo, queremos encontrar . Não precisa se assustar por ter uma letra no lugar do número não, é a mesma coisa que a questão anterior! Saca só:

E esse já é o final! Fica uma expressão grande assim mesmo porque eu não tenho como somar com ou subtrair . Como não tem essa possibilidade, essa fica sendo a nossa resposta pra essa parte da questão!

Vamos agora encontrar , é parecido com o que a gente viu no passo 2. Dá uma olhada:

Agora a gente pode dar mais uma ajeitada e mexer com os sinais negativos da expressão, como é o caso do ali que ta ao quadrado. Isso vai resultar na seguinte expressão final:

Nesse aqui queremos o . Começamos fazendo a mesma coisa que a gente fez nos passos anteriores de substituir:

Agora, vamos trabalhar com a expressão, expandindo o termo . Ele é um produto notável, ou seja, quando o expandirmos, vamos ter o quadrado do primeiro termo mais duas vezes o primeiro, vezes o segundo termo mais o quadrado do segundo termo. Lembrou? Fica com isso na cabeça que vai servir pra sempre! O termo é a mesma coisa que , o que a gente vai ajeitar na expressão também. Saca só:

Agora, a gente pega e multiplica por o que deve ser multiplicado:

Por fim, fata só a gente somar/subtrair os termos que são parecidos. Da uma olhada na nossa expressão final dessa parte:

Ta beleza? A gente já fez metade dos itens, bora em frente!

Vamos achar quem é . Como a gente achou no Passo 3, é só a gente pegar e multiplicar a expressão toda por , entendeu? Olha como fica:

A gente vai calcular nessa parte o , ou seja, iremos fazer na nossa expressão a substituição . Olha só:

Tudo que falta agora é calcular e substituir , que vale . Multiplicamos esse resultado por , o que vai resultar na seguinte expressão final:

Agora vamos lidar com o , logo, vamos fazer . Olha como fica a expressão inicial:

Para a expressão ficar do jeitinho que a gente quer, falta só ajeitar o . Nessa parte, a gente tem que lembrar que, quando a gente tem uma potência elevada a outra potência, multiplicamos os expoentes. Isso quer dizer que , ta ok? Resolvido isso, olha o que vai restar:

Para acharmos , temos que pegar a expressão de e multiplicar por ela mesma. Vai dar um pouco de trabalho, mas nada que a gene não consiga fazer com calma! Dá uma olhada:

Para fazer essa multiplicação a gente faz o famoso “chuveirinho”, multiplicando cada termo de dentro de um parêntese por cada termo de dentro do outro. Não ta lembrando? No caso do do primeiro parêntese, por exemplo, vamos multiplicar ele com os seguintes termos:

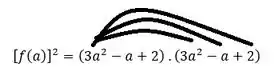
Relembrou? Pois é, a gente vai fazer isso pra todos os termos. No final, olha como fica essa multiplicação:

Ta cabando! Falta a gente só somar/subtrair os termos em comum e pronto! Vai ficar assim:

Última expressão, uhul! Falta só acharmos . A gente começa fazendo :

Agora, a gente expande o termo :

Fazemos, então, as devidas multiplicações:

E essa já é a nossa resposta final! :)