Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.2 - Ex. 22
Encontre :
Passo 1
Nesse caso, temos uma função dentro da outra e para resolver esse tipo de função devemos usar a Regra da Cadeira.
Podemos separar a função em e , e a derivada terá a seguinte aparência:
Onde chamamos de e :
Aplicando na Regra:
Para resolver esse problema, precisaremos primeiro resolver cada derivada separadamente e depois aplicamos na fórmula da Regra da Cadeia.
Passo 2
Para começar a calcular vamos nos atentar aos termos, onde:
Derivando primeiro a função em relação a :
E derivando em relação a :
Agora, é só aplicar os valores obtidos na Regra da Cadeia. Bora lá?
Passo 3
Vamos retomar os passos e aplicar na regra da Cadeia, onde:
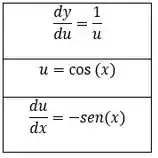
Agora, só aplicarmos os termos calculados na Regra:
Substituindo em :
Substituindo pela identidade trigonométrica que diz que :