Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.3 - Ex. 37
Se para encontre
Passo 1
Eaee, belezinha???
Bom... queremos determinar o seguinte limite:
E a única coisa que a gente sabe é que, para :
Tem ideia de como fazemos isso?
Muito bem galera, sabemos que a função está limitada superiormente por e inferiormente por
Então, para encontrar o limite da função vamos avaliar o limite quando tende a para ambos os extremos, que é o Teorema do Confronto!!
Lembrando que o teorema do confronto diz que:
Sejam , funções reais definidas no dominio e seja um ponto dentro desse dominio, se:
E
Então
Agora bora lá!! 😉
Passo 2
Começando pelo extremo inferior:
Usando a propriedade 2:
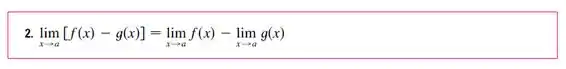
Agora vamos usar a propriedade de número 3:
Usando a de número 7 e 8:
Portanto, o limite inferior é
Sacou?
Passo 3
Para o extremo superior:
Usando as propriedades 1 e 2:
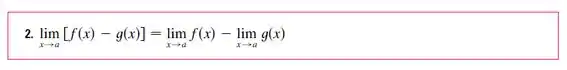
Agora a propriedade de número 3:
Usando a de número 7 e 8:
Agora vamos aplicar a última, número 9:
Logo, o limite superior é
Olha só que legal! O limite foi o mesmo para ambos os extremos, então, pelo teorema do confronto, o limite da função é 7!
E aí! entendeu tudo? Responde Aí!