Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 55
Se , encontre , , e . Trace , , e em uma mesma tela. Os gráficos são consistentes com as interpretações geométricas destas derivadas?
Passo 1
Faaala, gente bonita! Tudo certo por aí? Vamos dar uma olhada nessa questão! Ela traz essa função aqui:
O enunciado pede pra calcularmos todas essas derivadas aqui: , , e .
Segura o coração que ainda não acabou! Mas agora é mais tranquilo. Ele pede pra usarmos uma calculadora gráfica pra plotar os gráficos de , , e e checarmos se estão consistentes com a interpretação geométrica da derivada.
Beleza. Vamos utilizar a definição de derivadas pra calcular essas derivadas:
Mas e como fazemos pra calcular as derivadas de ordem superior?
Vamos pensar na derivada segunda, por exemplo. Só precisamos lembrar que a derivada segunda é a derivada da derivada. Então podemos dizer o seguinte:
As demais derivadas podem ser encontradas seguindo o mesmo raciocínio. Vamos lá!
Passo 2
Vamos começar, porque temos bastante coisa pra fazer!
Pra calcular a primeira derivada, vamos usar a definição:
Relembrando, a nossa função é essa aqui:
E podemos dizer que:
Aplicando no nosso limite, temos:
Realizando os produtos notáveis:
Simplificando os termos semelhantes:
Colocando o em evidência:
Agora finalmente calculando o limite:
Boa! Vamos pra próxima derivada!
Passo 3
Agora, podemos calcular da seguinte maneira:
Encontramos no passo anterior o resultado:
Podemos dizer que:
Substituindo no nosso limite, temos:
Realizando o produto notável:
Simplificando os termos semelhantes:
Colocando em evidência:
Calculando o limite:
Uhuuul!! Estamos chegando lá! Próxima derivada, aqui vamos nós!
Passo 4
Seguindo o raciocínio anterior, calculamos com a expressão:
Descobrimos que:
E sabemos que:
Substituindo no limite, temos:
Fazendo a todas as simplificações, temos:
Descobrimos a terceira derivada. Só falta mais uma!!
Passo 5
Vamos calcular assim:
Sabemos que:
E temos que:
Substituindo na definição:
Ufa! Conseguimos! Vamos agora pros gráficos.
Passo 6
Esboçando os gráficos, ficamos com (preto , lilás , vermelho e rosa ):
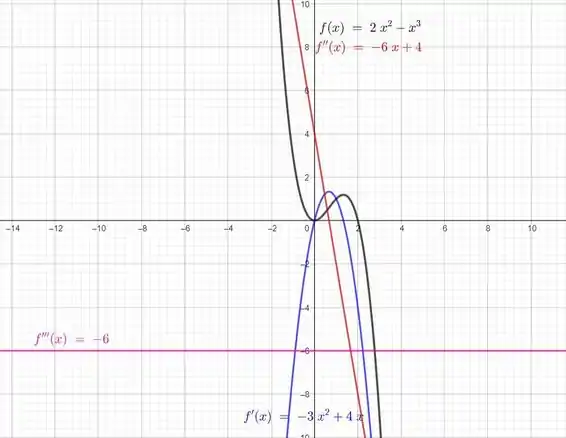
Para avaliarmos se faz sentido com o que encontramos, precisamos lembrar que a derivada de uma função representa a sua taxa de variação. Isso significa que:
Se a função for crescente, sua derivada será positiva.
Se a função for decrescente, sua derivada será negativa.
Percebemos que a função , em preto, tem o seguinte comportamento:
É decrescente pra ;
É crescente pra ;
É decrescente pra .
Isso significa que o gráfico da derivada , em lilás, precisa ter seus sinais da seguinte maneira:
Negativa pra ;
Positiva pra ;
Negativa pra .
E é exatamente o que encontramos no gráfico. Vamos continuar a nossa análise!
Podemos ver que a derivada tem o seguinte comportamento:
É crescente pra ;
É decrescente pra .
Isso significa que o gráfico da segunda derivada , em vermelho, precisa ter seus sinais da seguinte maneira:
Positiva pra ;
Negativa pra .
Também está batendo com o que encontramos no gráfico! Só falta mais uma análise!
A segunda derivada apresenta o seguinte comportamento:
É decrescente para todos os valores de .
Então os sinais da terceira derivada , em rosa, precisam se comportar assim:
Negativa para todos os valores de .
Também é o que encontramos no gráfico! Oba!
Conseguimos finalizar a nossa análise!