Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.3 - Ex. 54
encontre o ângulo , onde .
Passo 1
Beeem, a não ser que tenhamos uma calculadora, não temos como trabalhar com essa equação assim .rsrs. Precisamos alterar ela, mas como ? okay, ta vendo o ele tem que se transformar em alguma coisa de apenas . Assim a resolução fica mais simples.
A gente pode utilizar a fórmula do arco metade para resolver nosso problema :
Assim, equação fica:
Passo 2
Olha só! Melhoramos muito nossa equação, ela ta prontinha. Se a gente fizer uma substituição
Então nosso problema se resume em calularmos uma equação de segundo grau, coisas que já fizemos mil vezes. Então bora la!!!
Então
ou
Passo 3
Para , o pode assumir dois valores, e :
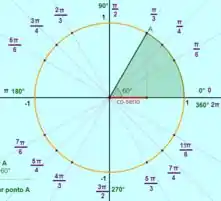
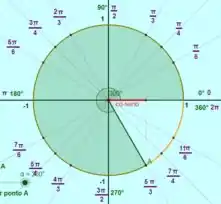
E para , o pode assumir somente um valor, :
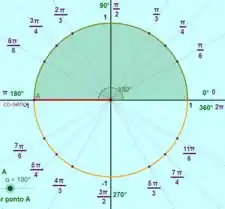
Prontinho terminamos aqui. Te encontro na próxima resolução, : )
Resposta
Exercícios de Livros Relacionados
Nos exercícios 39-42, expresse a quantidade em termos de sen x e cos x .42. co s 3 π 2 + x
37. O que acontece se você tomar a identidade trigonométrica cos A - B = cos A cos B + sen A sen B ? O resultado se parece com algo que você conhece?
43. Avalie sen 7 π 12 como sen π 4 + π 3
Nos exercícios 39-42, expresse a quantidade em termos de sen x e cos x .39. cos ( π + x )
43. Avalie co s 11 π 12 como co s π 4 + 2 π 3