Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.9 - Ex. 22

Encontre a antiderivada mais geral da função. (Verifique sua resposta por diferenciação.)

f x = 2 x 2 + 5 x 2 + 1

Passo 1

Primeiro vamos manipular a função fazendo a divisão dos polinômios:

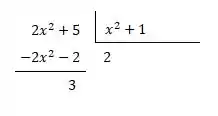
2 x 2 + 5 = 2 x 2 + 1 + 3 → 2 x 2 + 5 x 2 + 1 = 2 x 2 + 1 + 3 x 2 + 1 → 2 x 2 + 5 x 2 + 1 = 2 + 3 x 2 + 1

Assim temos que:

f x = 2 x 2 + 5 x 2 + 1 = 2 + 3 x 2 + 1

Vamos lá, sabemos que uma função F é chamada de antiderivada de f em um intervalo I se:

F ' x = f x

para todo x em I .

E se F é uma antiderivada de f nesse intervalo, então a antiderivada mais geral de f em I é:

F x + C

onde C é uma constante qualquer.

Pronto, então para achar a antiderivada, temos que achar uma função que derivando f nós encontramos F .

Passo 2

Vamos então agora calcular, para achar a antiderivada F da função f , temos que a antiderivada da função 1 1 + x 2 e de uma constante são da forma:

arctan ⁡ x

c x

Agora é só aplicar:

F x = 2 x + 3 ⋅ arctan ⁡ x + C = 2 x + 3 arctan ⁡ x + C

Passo 3

Vamos agora checar, para isso temos que derivar F x :

F ' x = 2 x 1 - 1 + 3 ⋅ 1 1 + x 2 + 0 = 2 x 0 + 3 1 + x 2 = 2 ⋅ 1 + 3 1 + x 2 = 2 + 3 1 + x 2 = 2 x 2 + 5 x 2 + 1

Pronto, tá tudo certo!

Resposta

F x = 2 x + 3 arctan ⁡ x + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

t)int (x^2 + 1)/(x) d x
1-Calcule.j)int root(3)(x ) d x
r) int ( 3 root(5)(x^2) + 3 ) d x
o) int (3 x^2 + x + (1)/(x^3)) d x
s)int (2 x^3 - (1)/(x^4)) d x