Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.10 - Ex. 6
Encontre a aproximação linear da função em e use-a para aproximar os números e . Ilustre fazendo os gráficos de e da reta tangente
Passo 1
E aee, belezinha?? Então.. a questão quer que a gente encontre a aproximação linear da seguinte função em :
Para isso, devemos aplicar a seguinte fórmula da linearização
Com essa aproximação linear, devemos utilizar para aproximar os números e .
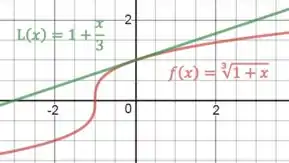
Por fim, vamos plotar o gráfico de e da reta tangete.
Passo 2
Para obter a linearização uma função , devemos utilizar a aproximação da função em :
Para isso vamos derivar :
Passo 3
Então, em é:
Passo 4
Agora, para os números e temos:
- :
2) :
Passo 5
Para ilustrar a situação, temos o gráfico:
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 7-14, determine uma linearização em um inteiro escolhido convenientemente próximo a x 0 em que a função dada e sua derivada sejam fáceis de calcular.14- f x = s i n x - 1, x 0 = π 12
Aproximações lineares comuns em x = 0 Determine as linearizações das seguintes funções em x = 0. t gx
Nos Exercícios 7-14, determine uma linearização em um inteiro escolhido convenientemente próximo a x 0 em que a função dada e sua derivada sejam fáceis de calcular.10- f x = 1 + x, x 0 = 8.1
Aproximações lineares comuns em x = 0 Determine as linearizações das seguintes funções em x = 0 .d) e x
Calcule a integral int ϴ . c o s ( pi . ϴ ) d ϴ ϴ ϴ ϴ usando integração por partes.