Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.5 - Ex. 3
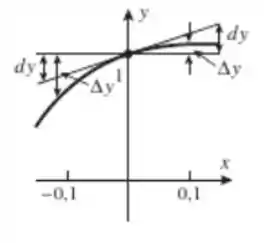
(a) Encontre a aproximação linear local da função em e use-a para aproximar e
(b) Faça o gráfico de e de sua reta tangente em e use-os para ilustrar a relação entre os valores exatos e as aproximações de e
Passo 1
(a)
Sabemos perla Fórmula (1) que para aproximarmos usamos:
Fazendo pra em teremos:
Achando a derivada da função:
Substituindo tudo isso dentro da Fórmula (2):
Passo 2
Para aproximar usando a expressão que encontramos, mas , ou seja, vamos usar que , pois:
Colocando na expressão:
Passo 3
Para aproximar o pensamento vai ser análogo, colocaremos pois:
Colocando na expressão:
Passo 4
(b)
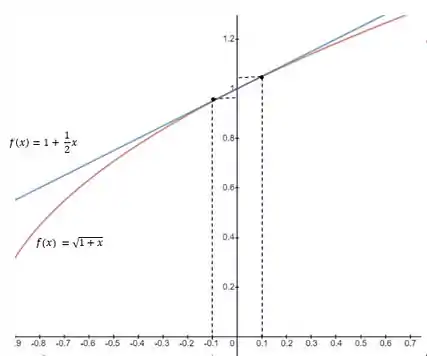
Os valores aproximados estão praticamente em cima dos valores exatos, o que indica ser uma aproximação muito boa 😊
Se dermos um ”zoom” para entender a aproximação, vamos ver que na verdade é mais ou menos assim:
Passo 5
