Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 48
Um bote deixa uma doca às horas da tarde e viaja na direção sul a uma velocidade de . Outro bote está indo para a direção leste a e atinge a mesma doca às horas da tarde. Em que momento os dois botes estavam mais próximos um do outro?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar o momento em que os dois botes estavam mais próximos um do outro, sabendo que um dele deixa a doca às horas da tarde e viaja na direção sul a uma velocidade de , enquanto o outro está indo na direção leste a e atinge a mesma doca às horas da tarde.
Com essas informações esboçamos o seguinte desenho:
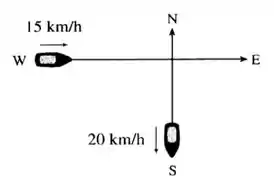
Vamos chamar de o tempo, em horas, após duas da tarde. A posição do barco indo para o sul é , porque a primeira posição é na origem e a segunda é após se afastar a .
A posição do barco indo para leste é , sendo a primeira posição antes da origem, andando a , e a segunda, a origem.
Se chamados de a distância entre os barcos no momento , o que nós vamos fazer é minimizar a distância:
Vamos lá!
Passo 2
Vamos começar derivando a nossa função em relação a :
E igualando esse resultado a zero, temos:
Isolando , ficamos com:
Transformando isso para minutos, vamos ter:
Ou seja:
Como é maior que zero, esse ponto realmente é um valor mínimo, então, os barcos estão mais próximos em .
Valeu, galera! Até a próxima! 😉