Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.6 - Ex. 61

Encontre a área da parte da esfera x 2 + y 2 + z 2 = 4 z que está dentro do parabolóide z = x 2 + y 2 .

Passo 1

Oioi pessoal, vamos começar entendendo o que o exercício quer. Bom ele pede para que a gente encontre a área da parte da esfera x 2 + y 2 + z 2 = 4 z que está dentro do parabolóide z = x 2 + y 2 .

Para isso podemos usar a integral dupla que representa a área da superfície:

A S = ∫ ∫ D   1 + ∂ z ∂ x 2 + ∂ z ∂ y 2   d A

Bom, então iremos começar achando as derivadas parciais ∂ z ∂ x e ∂ z ∂ y e depois substituiremos na integral.

Depois iremos parametrizar em coordenadas polares para ficar mais fácil de achar os limites de integração .

Feito isso, é só pôr a mão na massa e resolver a conta.

Vamos começar!

Passo 2

Vamos achar quem são essas derivadas parciais ∂ z ∂ x e ∂ z ∂ y . Ish, mas você percebeu que temos que ter uma equação para z ? Bom isso não será um problema , temos que isolar o z .

Podemos ajustar a equação somando + 4 dos dois lados de forma que podemos escrever ( z 2 - 4 z ) em forma de produto notável.

x 2 + y 2 + z 2 - 4 z = 0

Somando:

x 2 + y 2 + z 2 - 4 z + 4 = 4

E isso é a mesma coisa que

x 2 + y 2 + z - 2 2 = 4

Agora vamos passar tudo para o outro lado:

z - 2 2 = 4 - x 2 + y 2

Passando o expoente em forma de raiz:

z - 2 = 4 - x 2 - y 2

z = 2 + 4 - x 2 - y 2

Show, agora temos uma equação de z .

Passo 3

Agora sabemos que z = 2 + 4 - x 2 - y 2 , vamos achar as derivadas parciais.

Começando por ∂ z ∂ x :

∂ z ∂ x = ∂ ∂ x 2 + 4 - x 2 - y 2

Aí a gente vai usar uma regrinha da cadeia e vamos ficar com:

- 1 2 4 - x 2 - y 2 . 2 x

Então temos que

∂ z ∂ x = - x 4 - x 2 - y 2

Agora para ∂ z ∂ y :

∂ z ∂ y = ∂ ∂ y 2 + 4 - x 2 - y 2

E pra ∂ z ∂ y   é basicamente a mesma coisa hehe, só que em relação a y .

Nosso resultado final fica:

∂ z ∂ x = - y 4 - x 2 - y 2

Vamos substituir na nossa integral:

A S = ∫ ∫ D   1 + ∂ z ∂ x 2 + ∂ z ∂ y 2   d A

Ficaremos com:

A ( s ) = ∫ ∫ D   1 + - x 4 - x 2 - y 2 2 + - y 4 - x 2 - y 2 2   d A

Passo 4

Shoow agora a gente pode mandar isso pra nossa integral

A ( s ) = ∫ ∫ D   1 + - x 4 - x 2 - y 2 2 + - y 4 - x 2 - y 2 2   d A

Vamos elevar as derivadas parciais ao quadrado:

A ( s ) = ∫ ∫ D   1 + x 2 ( 4 - x 2 - y 2 ) 2 + y 2 ( 4 - x 2 - y 2 ) 2   d A

Se ajeitarmos essa integral feiosa, ficamos com

A ( s ) = ∫ ∫ D   1 + x 2 + y 2 4 - ( x 2 + y 2 )   d A

Passo 5

Beleza galera, agora precisamos passar tudo para coordenadas polares:

x = r   c o s   ( θ )

y = r   s e n   ( θ )

e

d A = r d r d θ

Esse valor é sempre o mesmo para coordenadas polares mas achamos através da fórmula:

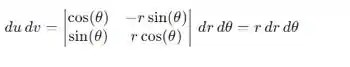
Substituindo os novos valores na integral:

A ( s ) = ∫ ∫ D   1 + x 2 + y 2 4 - ( x 2 + y 2 )   d A

teremos:

A ( s ) = ∫ ∫ D   1 + ( r   c o s   ( θ ) ) 2 + ( r   s e n   ( θ ) ) 2 4 - ( ( r   c o s   ( θ ) ) 2 + ( r   s e n   ( θ ) ) 2 )   r d r d θ

Parece assustador, porém olha só esse bizu.Normalmente quando temos s e n 2 θ   e   c o s 2   θ em um mesmo problema podemos tentar juntá los de tal forma para substituir por s e n 2 θ   +   c o s 2   θ = 1 .

Sendo assim:

A ( s ) = ∫ ∫ D   1 + r 2 s e n 2   θ + r 2   c o s 2 θ 4 - ( r 2 s e n 2   θ + r 2   c o s 2 θ )   r d r d θ

Logo:

A ( s ) = ∫ ∫ D   1 + r 2 ( s e n 2 θ   +   c o s 2   θ ) 4 - r 2 ( s e n 2 θ   +   c o s 2   θ )   r d r d θ

Olha quem apareceu ali, dessa forma:

A ( s ) = ∫ ∫ D   1 + r 2 4 - r 2   r d r d θ

Passo 6

Show, mas ainda precisamos achar nossos limites de integração

O de θ é tranquilinho, como o enunciado não dá nenhuma restrição ele dá a volta completa no eixo z , então nós temos que

0 ≤ θ ≤ 2 π

Já o de r a gente vai precisar de um jeitinho especial para achar.

Lembra que a nossa esfera x 2 + y 2 + z 2 = 4 z está dentro do parabolóide z = x 2 + y 2 ??

Isso quer dizer que precisamos encontrar o valor de acordo com o parabolóide. Vamos ver graficamente só para você sacar o que eu estou falando.

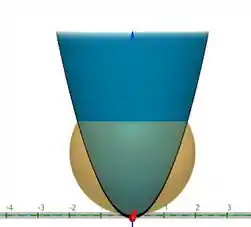
Queremos achar a área que corresponde a parte que está verde , e os nossos limites de integração será a parte pretinha, entendeu?

Para a gente encontrar esse valor teremos que igualar nossas duas funções, temos que

x 2 + y 2 + z 2 = 4 z   e que z = x 2 + y 2

então podemos dizer que:

z + z 2 = 4 z

z 2 - 3 z = 0

z z - 3 = 0

Então chegamos que

z = 0 ou z = 3

Só que quem é z mesmo?

z = x 2 + y 2

Que nas nossas coordenadas polares é a mesma coisa que

z = ( r   c o s   ( θ ) ) 2 + ( r   s e n   ( θ ) ) 2

z = ( r   c o s   ( θ ) ) 2 + ( r   s e n   ( θ ) ) 2

z = r 2 ( s e n 2 θ   +   c o s 2   θ )

Logo:

z = r 2

Então uhul achamos nossos limites

0 ≤ r ≤ 3

Passo 7

Agora vamos resolvê-la:

∫ 0 2 π ∫ 0 3 1 + r 2 4 - r 2   r   d r   d θ

Separando as raízes:

∫ 0 2 π ∫ 0 3 1 + r 2 4 - r 2 r   d r   d θ

Logo:

∫ 0 2 π ∫ 0 3 2 r 4 - r 2   d r   d θ

Sempre começamos pela ordem de dentro para fora, ou seja, vamos integral primeiro em relação a r :

∫ 0 3 2 r 4 - r 2   d r

Vamos fazer uma substituição simples e chamar

u = 4 - r 2

d u = ( 4 - r 2 ) ' d r

d u = 2 r   d r

Substituindo na integral:

∫ 0 3 2 r u 2 r   d u

logo:

∫ 0 3 1 u   d u

- 2 u 1 2 0 3

Retornando com u = 4 - r 2 :

- 2 4 - r 2 1 2 0 3

- 2 4 - ( 3 ) 2 1 2 - 4 - ( 0 ) 2 1 2

- 2 4 - 3 1 2 - 4 1 2

- 2 1 - 2

Logo:

∫ 0 3 2 r 4 - r 2   d r = 2

Substituindo em:

∫ 0 2 π ∫ 0 3 2 r 4 - r 2   d r   d θ

teremos:

∫ 0 2 π 2 d θ

Passo 8

Agora para fechar vamos resolver:

∫ 0 2 π 2   d θ

2 θ 0 2 π

2.2 π - 2.0

Logo:

A S = ∫ 0 2 π ∫ 0 3 1 + r 2 4 - r 2   r   d r   d θ = 4 π

A S = 4 π

Resposta

A S = 4 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Use a Regra do Ponto Médio para integrais duplas (veja a Seção 15.1 ) com seis quadrados para estimar a área da superfície z = 1 1 + x 2 + y 2,0 ≤ x ≤ 6,0 ≤ y ≤ 4 .(b) Use um sistema de computação
Determine a área exata da superfície z = 1 + 2 x + 3 y + 4 y 2, 1 ≤ x ≤ 4, 0 ≤ y ≤ 1
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A parte da superfície z = e
Determine, com precisão de quatro casas decimais, a área da parte da superfície z = 1 + x 2 1 + y 2 que está acima do quadrado x + y ≤ 1 . Ilustre, traçando o gráfico dessa parte da superfície.
(a) Mostre que as equações paramétricas x = as e nu cos ⁡ u,y = bs e nus e nv,z = c cos ⁡ u,0 ≤ u ≤ π,0 ≤ v ≤ 2 π , representam um elipsoide.(b) Use as equações paramétricas da parte (a) para traçar o