Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.6 - Ex. 54
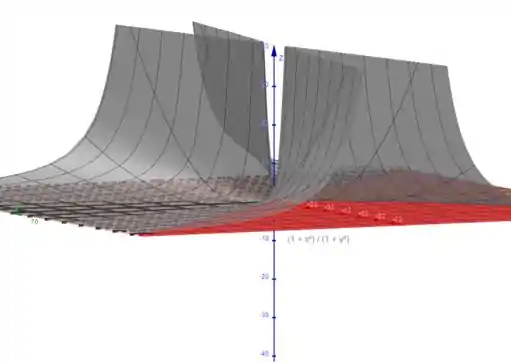
Determine, com precisão de quatro casas decimais, a área da parte da superfície que está acima do quadrado . Ilustre, traçando o gráfico dessa parte da superfície.
Passo 1
Fala galera, beleza!?
Com precisão de quatro casas decimais precisamos determinar a área da superfície:
Que está acima do quadrado:
Também, ilustrar o gráfico dessa superfície.
Vamos com calma pessoal!
Primeiro vamos lembrar como podemos expressar a área de superfície. Temos a seguinte fórmula:
Onde,
Nossa região D, é a região delimitada pelo quadrado:
Podemos isolar , e lembrar que modulo podemos escrever como mais ou menos. Ficando assim:
Assim, temos o intervalo de integração em .
Para achar o intervalo de integração em , verificamos quando for zero. Assim:
Repare que também já temos a função , basta fazermos as derivadas em relação a e e substituir na integral.
Para resolver essa integral, você pode usar o WolframAlpha ou algum outro software de sua preferência. Já para esboçar o gráfico, vamos utilizar o Geogebra 3D, mas você pode utilizar outro software.
Então, vamos nessa pessoal!
Passo 2
Vamos começar reorganizando nossa integral.
Onde,
A função é:
Fazendo a derivada em relação , temos:
Já em relação , vamos ter:
Nossos limites de integração são:
Como a variável possui uma função em seu limite que depende de , vamos ter que integrar primeiro em .
Ficando assim nossa integral:
Passo 3
Nosso objetivo é resolver essa integral.
Como recomendação do livro, devemos utilizar um software.
Utilizando o WolframAlpha, vamos entrar com o seguinte input:
Integrate[Sqrt[1+(2x/(1+y^2 ))^2+(-2y(1+x^2 )/(1+y^2 )^2 )^2],{y,-(1-|x|),1-|x|},{x,-1,1}]
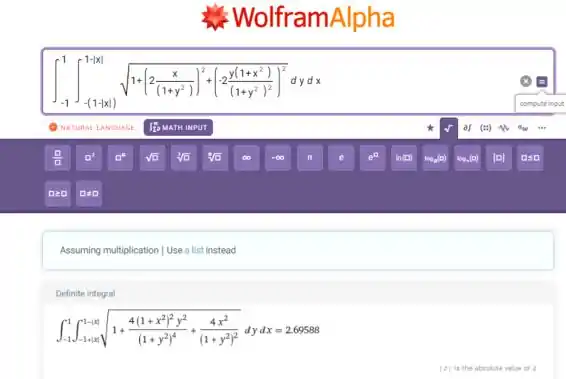
Utilizando um sistema de computação algébrica, estimamos a integral e nosso resultado dá:
Passo 4
Agora, vamos fazer um esboço dessa superfície.
Acima do quadrado .
Entrando com essas funções no Geogebra 3D, vamos obter o seguinte gráfico:
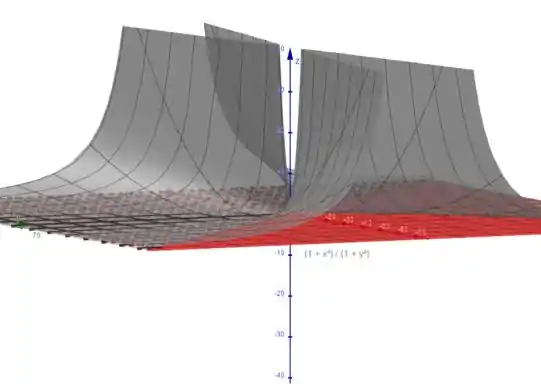
Em cinza temos a superfície , e em vermelho o quadrado que delimita a superfície.
Repare que é um gráfico chatinho de fazer a mão, por isso a necessidade de um software gráfico.
Resposta
