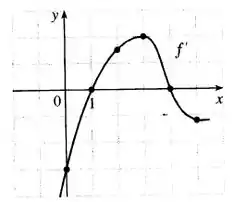
Use ao gráficos dados para estimar o valor de cada dereivada. Esboce então o gráfico de .
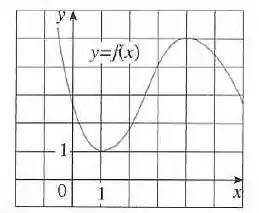
Passo 1
Vamos analisar o gráfico para estimar os valores:
- No ponto a tangente tem uma inclinação negativa e deve ficar em torno de , assim, .
- No ponto a tangente tem uma inclinação horizontal, fazendo ela ter valor , assim, .
- No ponto a tangente tem uma inclinação positiva e deve ficar em torno de , assim, .
- No ponto a tangente tem uma inclinação positiva e deve ficar em torno de , assim, .
- No ponto a tangente tem uma inclinação horizontal, fazendo ela ter valor , assim .
- No ponto a tangente tem uma inclinação negativa e deve ficar em torno de , .
Passo 2
Passo 3
Passo 4
Passo 5
Passo 6
Passo 2
Agora vamos esboçar o gráfico de :