Encontre a área da região delimitada pelas curvas dadas:
Passo 1
Opa! Nessa questão o enunciado pede pra que a gente encontre a área da região delimitada pelas curvas dadas:
Só pra ficar mais claro, vamos desenhar um esboço dessas funções:
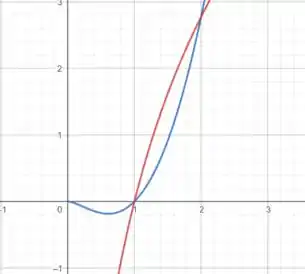
Passo 2
Agora precisamos descobrir os limites de integração, para isso vamos calcular os pontos onde as curvas e se interceptam:
Observe que não consideramos o valor de , pois não existe logaritmo natural de número negativo, logo nosso domínio é restrito a e esse valor não pertence a ele.
Passo 3
Logo temos que o intervalo de interceção é e assim a área entre essas curvas é dada por:
Para este caso vamos aplicar a técnica de integração por partes. Para isso precisamos dividir o argumento da integral em duas funções e respectivamente. Feito isso, aplicamos a fórmula para a integração por partes que é dada por :
Ou de forma mais visível, fazemos:
Primeiro então, devemos definir quem vão ser nossas funções. É aconselhável escolher a função mais fácil de derivar para ser ou a mais difícil de se integrar. Assim:
Derivando e integrando , temos:
Passo 4
Aplicando as funções e suas derivadas na fórmula citada no passo anterior, temos:
Relembrando que de forma genérica a integral definida possui a seguinte definição:
Ou seja, após integrar de forma genérica você irá substituir os limites de integração ( a e b) nesse resultado obtido, respeitando a ordem de o limite superior aplicado na função menos o limite inferior aplicado na função.