Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.5 - Ex. 61
Encontre a área da região delimitada pela hipérbole e pela reta vertical passando por um foco.
Passo 1
Bom, pessoal. Primeiro temos que identificar como é essa figura cuja área queremos calcular. Já sabemos que parte da fronteira dessa figura é dada pela hipérbole de equação:
A outra parte da fronteira é uma reta vertical, então sua equação é da forma:
Mas quem é essa constante? Bom, o exercício nos disse que essa reta passa por um foco, então podemos dizer que:
Se escolher o foco da região positiva , ficamos com:
E fazendo um esboço, a área que queremos calcular fica mais clara:
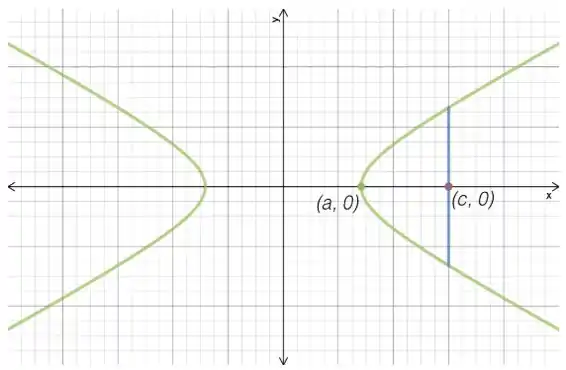
Passo 2
Show! Agora repare que a hipérbole é simétrica em relação ao eixo , ou seja, o que acontece em cima, também acontece em baixo. Portanto, pra facilitar a nossa vida, podemos calcular só a área da parte de cima da figura, e depois multiplicar por .
Então, pra achar a área dessa parte, podemos integrar a função que corresponde a essa parte da hipérbole, com indo de até .
Mas que função representa a hipérbole? No passo anterior, achamos:
Mas uma função não pode nos dar dois valores de pra cada . Então a gente pega só a parte positiva, pois estamos calculando a área da metade de cima da figura, onde , beleza?
Nossa integral fica assim então:
Passo 3
Agora, como que a gente faz pra calcular aquela integral?
Bom, ela é realmente complicada de se fazer no braço. Então vamos usar a Tabela de Integrais do livro, , pra descobrir que:
Agora a gente consegue calcular!
Mas, pra hipérbole, a gente sabe que , então:
Pra descobrir a área total, é só multiplicar o resultado por , né?
onde .