Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 33
Encontre a área da região que está dentro de ambas as curvas
Passo 1
Olá, meu querido e amado amigo, vamos resolver juntos mais uma atividade hoje.
Temos em mãos duas curvas:
E queremos saber a área da região que está simultaneamente dentro dessas duas curvas.
A gente tem em mãos uma família de lemniscata, que possui equações do tipo:
As que possuem cosseno são posicionadas em simetria com o eixo para com o eixo com . Já as que possuem seno são posicionadas com simetria com o e com com .
Vamos plotar as curvas para termos ideia da área que a gente tá calculando.
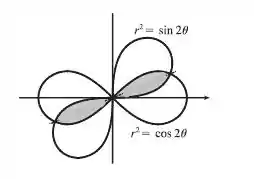
Portanto, queremos a área dessa região sombreada.
A área de uma curva em coordenadas polares é dada por:
Então temos que identificar cada termo dessa integral aí, substituir e calcular.
Para encontrar esse intervalo, no caso dessa questão, vamos precisar encontrar os pontos de interseção das duas curvas, já que queremos a área dentro de ambas as curvas.
Passo 2
Para isso, basta igualarmos as duas curvas para encontrarmos:
Então vamos pensar. Eu sei que a região sombreada não está só no primeiro quadrante, mas por hora, vamos focar só no primeiro quadrante.
Se a gente imaginar uma reta bem no ponto de interseção entre as duas curvas, é como se nossa região sombreada fosse a curva de até e depois passasse a ser a curva , de até .
Vê se você consegue visualizar isso:
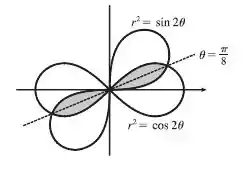
Acontece que, se aproveitando de que existe uma simetria, a gente pode dividir nossa região sombreada em áreas e cada uma dessas áreas, em partes, bem no meio e só calculamos a área de até e depois a gente multiplica isso por , ok?
Passo 3
Continuando, falta a gente descobrir quem é o .
O é a própria parametrização.
Mas agora a gente precisa ficar esperto. Como dividimos nossa curva em partes e só vamos calcular a integral de até , temos que nos atentar, como a gente tinha conversado ali em cima, que nesse intervalo a nossa região de interesse é definida apenas pela curva
Assim, esse é o nosso .
Então agora é só substituir e integrar esse negócio.
Passo 4
Vamos l��:
Integrando:
Colocando os limites de integração:
Colocando os valores dos cossenos:
Assim, a área total da nossa região é