Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 30
Encontre a área da região que está dentro de ambas as curvas
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu as seguintes equações polares:
Queremos calcular a área da região intersectada pelas duas curvas.
Vamos plotar as curvas para termos ideia da área que a gente tá calculando (a gente pegar os limites de integração dessa figura.. a gente vai encontrar eles no braço haha):
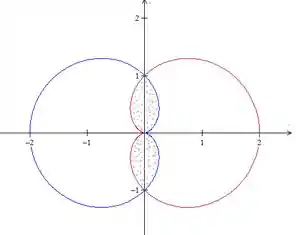
Portanto, queremos a área dessa região pontilhada.
Para calcular isso, sabemos que a área de uma curva em coordenadas polares é dada por:
Então temos que identificar cada termo dessa integral aí, substituir e calcular.
Já para determinar os limites de integração, a gente vai ter que calcular os pontos de interseções entre as curvas, certinho?? Agora bora lá! 😉
Passo 2
O intervalo de integração seria o intervalo em que a curva está definida.
Para encontrar esse intervalo, no caso dessa questão, vamos precisar encontrar os pontos de interseção das duas curvas, já que queremos a área dentro de ambas as curvas.
Para isso, basta igualarmos as duas curvas:
Ou
Assim, esses são os dois valores de no qual as curvas se intersectam, logo, vai ser o intervalo no qual nossa região de interesse está definida:
Então, o intervalo de integração é
Maaaas, se você reparar, nossa região pontilhada é simétrica!
Logo, podemos dividir ela em quatro e calcular a área de até e depois multiplicar por quatro pra ter a área total, o que acham?
Isso vai facilitar nossa vida na hora de fazer a integral!!
Passo 3
Continuando, falta a gente descobrir quem é o .
O é a própria parametrização.
Mas agora a gente precisa ficar esperto.
Como dividimos nossa curva em 4 partes e só vamos calcular a integral de até , temos que nos atentar que nesse intervalo a nossa região de interesse é definida apenas pela curva azul!
E eu não tinha dito pra você ainda, mas a curva azul é a curva:
Assim, esse é o nosso .
Então agora é só substituir e integrar esse negócio.
Passo 4
Vamos lá:
Abrindo a expressão, temos:
Tem uma relação trigonométrica que diz que . Assim, substituindo, temos:
Aplicando a integral:
Aplicando os limites de integração:
Assim, a área total da nossa região é: