Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 17
Encontre a área da região dentro de um laço da curva:
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte equação polar que descreve uma curva:
Queremos calcular a área da região dentro de um dos laços dessa curva.
Mas como assim dentro de um dos laços??
A curva tem formato de um trevo de três folhas. E queremos encontrar a área de uma das “folhas”, conforme mostra a figura abaixo:
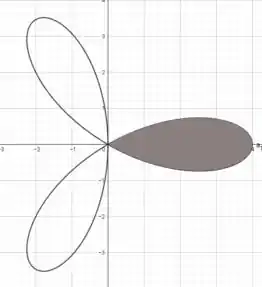
Essa figura foi colocada só para a gente enxergar melhor o que queremos calcular.
Como queremos encontrar uma área de uma curva que é dada em coordenadas polares, temos que:
Agora bora aplicar!! 😉
Passo 2
Primeiro vamos encontrar os limites de integração!!
A curva passa pela origem quando seu raio é , dessa forma podemos fazer:
Dessa forma, nossos limites de integração são e .
Passo 3
Para calcular a área abaixo de uma curva, lembramos que:
Substituindo :
Passo 4
Lembrando que:
Temos:
A primeira integral é dada por:
Já na segunda integral, podemos fazer por substituição simples. Seja:
Assim podemos reescrever a integral como:
Voltando para a variável original temos:
Assim, a área procurada é a soma dessas 2 integrais, ou seja:
Resposta
A área abaixo da curva é