Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.4 - Ex. 15

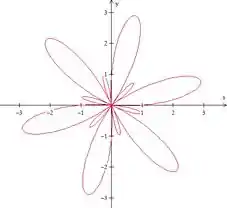
Trace a curva com uma ferramenta gráfica e calcule a área limitada por ela

r = 1 + 2 sen ⁡ 6 θ

Passo 1

Olá, meu amigo. Vou te ajudar a resolver essa atividade.

Aqui a gente tem a curva:

r = 1 + 2 sen ⁡ 6 θ

E deveremos utilizar uma ferramenta gráfica para plotar essa figura, e também deveremos calcular a área dela.

A área de uma curva em coordenadas polares é dada por

A = ∫ a b 1 2 r 2 d θ

Olhando essa integral, a gente não tem os intervalos ainda, iremos descobri-los a partir do esboço da nossa figura.

Primeiro vamos traçar nossa curva, depois a gente calcula a área.

Com a ajuda do Winplot, nossa curva fica:

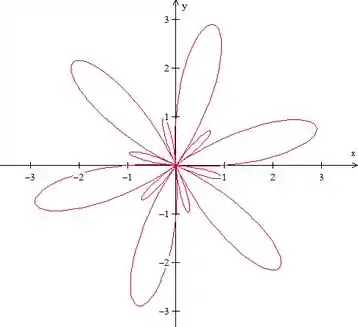
Essa coisa lokona aí....

Passo 2

Agora sim vamos calcular a área da curva!

Como foi dito, a área de uma curva em coordenadas polares é dada por

A = ∫ a b 1 2 r 2 d θ

Então temos que identificar cada termo dessa integral aí, substituir e calcular.

O intervalo de integração seria o intervalo total da nossa figura, ela começa em:

a = 0

E vai até:

b = 2 π

Continuando, o r é a própria parametrização:

r = 1 + 2 sen ⁡ 6 θ

Então é só substituir e integrar esse negócio.

Passo 3

Vamos lá:

A = 1 2 ∫ 0 2 π 1 + 2 sen ⁡ 6 θ 2 d θ

Realizando o produto notável:

A = 1 2 ∫ 0 2 π ( 1 + 4 sen ⁡ 6 θ + 4 sen 2 ⁡ 6 θ ) d θ

Dividindo a integral em 3:

A = 1 2 ∫ 0 2 π d θ + 1 2 ∫ 0 2 π 4 sin ⁡ 6 θ d θ + 1 2 ∫ 0 2 π 4 sin 2 ⁡ 6 θ d θ

Calculando as duas primeiras integrais, que são mais fáceis e utilizando da identidade trigonométrica:

sin 2 ⁡ x = 1 - cos ⁡ 2 x 2

A = 1 2 2 π - 0 - 1 2 ⋅ 4 ⋅ 1 6 ⋅ cos ⁡ 6 θ ​ 0 2 π + 1 2 ∫ 0 2 π 4 1 - cos ⁡ 12 θ 2 d θ

Separando novamente a integral:

A = π - 1 3 cos ⁡ 12 π - 1 3 cos ⁡ 0 + 1 2 ⋅ 4 ⋅ 1 2 ∫ 0 2 π d θ - ∫ 0 2 π cos ⁡ 12 θ d θ

Calculando as integrais restantes:

A = π + 1 2 π - 0 - sin ⁡ 24 π - sin ⁡ 0

A = π + 1 2 π - sin ⁡ 24 π - sin ⁡ 0

A = 3 π

Resposta

A = 3 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a curva x = t + t 3y = t - 1 t 2 1 ≤ t ≤ 2 girar em torno do eixo x , estime a área da superfície resultante com precisão de três casas decimais.
Calcule a área da superfície gerada pela rotação da curva dada em torno do eixo y .66. x = e t - t , y = 4 e t 2 ,0 ≤ t ≤ 1
Encontre a área exata da superfície obtida pela rotação da curva dada ao redor do eixo x.59. x = t 3 ,y = t 2 , 0 ≤ t ≤ 1
Escreva, mas não calcule, uma integral que represente a área da superfície obtida pela rotação da curva dada ao redor do eixo x.57. x = s e n 2 t ,y = s e n3 t , 0 ≤ t ≤ π / 3
Encontre a área exata da superfícies obtida pela rotação da curva dada ao redor do eixo x . x = 3 t - t 3 ,y = 3 t 2 , 0 ≤ t ≤ 1