Enunciado
Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 10.4 - Ex. 26
Encontre a área da região que está dentro da primeira curva e fora da segunda curva.
Passo 1
Eaeee, tudo tranquilinho?? Bom... o enunciado nos deu duas expressões (dadas em coordenadas polares):
Queremos calcular a área da região que está dentro da primeira curva e fora da segunda curva, ou seja:
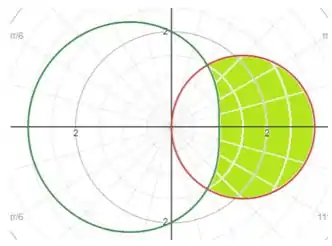
Obs, a curva em vermelho é e a curva em verde é .
Portanto, queremos a área dessa região hachurada.
Para isso, devemos saber que a área de uma curva em coordenadas polares é dada por:
Então temos que identificar cada termo dessa integral aí, substituir e calcular.
Então vamos começar procurando os intervalos de integraçõ!! 😉
Passo 2
O intervalo de integração seria o intervalo em que a curva está definida.
Para encontrar esse intervalo, no caso dessa questão, vamos precisar encontrar os pontos de interseção entre as duas curvas.
Para isso, igualamos as duas curvas:
Com isso, temos os seguintes resultados:
Ou
Assim, esses são os dois valores de no qual as curvas se intersectam, logo, vai ser o intervalo no qual nossa região de interesse está definida:
Então, o intervalo de integração é
Maaaas, se você reparar, nossa região sombreada é simétrica!
Logo, podemos dividir ela em duas e calcular a área de até e depois multiplicar por dois pra ter a área total, o que acham?
Isso vai facilitar nossa vida na hora de fazer a integral!!
Passo 3
Continuando, falta a gente descobrir quem é o .
O é a própria parametrização. Mas como queremos descobrir a área entre a primeira e a segunda curva, vê se faz sentido pra vocês que a gente faça a área da curva de fora menos a área da curva de dentro?
Faz né?!
Assim, vamos ter dois , porque vamos ter duas áreas, ou seja, duas integrais, a da curva de fora e a da curva de dentro.
Então agora é só substituir e integrar esse negócio.
Passo 4
Vamos lá:
Como aqui a gente tá com duas integrais grandes com intervalos iguais. Vamos juntar elas pra ver se corta alguma coisa e facilita a nossa vida:
Sabemos que , logo:
Sabemos que a integral do cosseno é o seno. Assim, resolvendo a integral, temos:
Aplicando os limites de integração:
Assim, a área total da curva é