Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.2 - Ex. 33

Enocontre a área limitada pela curva x = cos ⁡ t e y = e t , 0 ≤ t ≤ π / 2 e as retas y = 1 e x = 0 .

Passo 1

O problema fornece a curva parametrizada

x = cos ⁡ t             e               y = e t

E pede a área da região limitada pela curva e pelas retas x = 0 e y = 1 . A seguir plotamos as duas curvas:

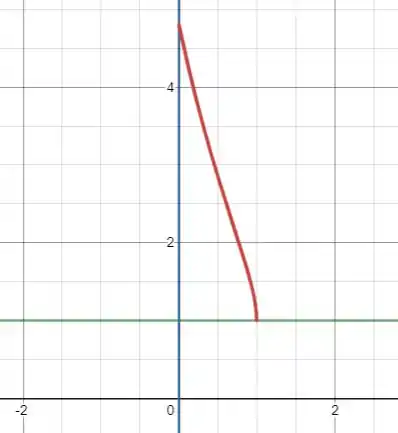
Queremos a área da região abaixo da curva e acima da reta y = 1 ! Assim,

A = A 1 - A 2 ,

onde A 1 é a área abaixo da curva e A 2 é a área do retângulo abaixo da reta y = 1 .

Passo 2

A área do retângulo será

A 2 = 1 ⋅ 1 = 1

Já para a área sobre a curva parametrizada, usamos o método ensinado nesse capítulo:

A 1 = ∫ a b y   d x = ∫ α β y t   x ' t   d t

Nesse caso, α = 0 e β = π / 2 :

A 1 = ∫ 0 π / 2 e t ⋅ - s e n   t   d t = - ∫ 0 π / 2 e t   s e n   t   d t

Para calcular essa integral usamos integração por partes:

∫ u   d v = u v - ∫ v   d u

Vamos chamar u = e t e d v = - s e n   t   d t :

d u = e t   d t                 e               v = cos ⁡ t

Logo,

A 1 = e t cos ⁡ t 0 π 2 - ∫ 0 π 2 e t cos ⁡ t   d t = - 1 - ∫ 0 π / 2 e t cos ⁡ t   d t

Aplicamos partes novamente na segunda integral:

u = e t             e               d v = cos ⁡ t   d t

Assim,

d u = e t   d t           e           v = s e n   t

Logo,

A 1 = - 1 - e t s e n   t 0 π 2 - ∫ 0 π 2 e t   s e n   t   d t = - 1 - e π 2 + A 1

Portanto,

A 1 = - 1 - e π 2 - A 1 ⇒ A 1 = - 1 - e π 2 2

O sinal negativo apareceu pois integramos no sentido invertido, basta tomar o módulo pois uma área sempre é positiva:

A 1 = 1 + e π / 2 2

Desta forma, a área pedida será

A = A 1 - A 2 = 1 + e π 2 2 - 1

Portanto,

A = e π 2 - 1 2

Resposta

A = e π 2 - 1 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Assumindo que as equações nos Exercícios 15-20 definem x e y implicitamente como funções deriváveis x = f ( t ) ,y = g ( t ) , encontre o coeficiente angular da curva x = f ( t ) ,y = g ( t ) no valor
Assumindo que as equações nos Exercícios 15-20 definem x e y implicitamente como funções deriváveis x = f ( t ) ,y = g ( t ) , encontre o coeficiente angular da curva x = f ( t ) ,y = g ( t ) no valor
22. Encontre a área delimitada pelo eixo y e a curva: x = t - t 2 ,y = 1 + e t .
Encontre as áreas das regiões nos Exercícios 1-8Delimitada pela espiral r = θ para 0 ≤ θ ≤ π .
Encontre os comprimentos das curvas nos exercícios 21-28.A espiral r = e θ / 2 ,0 ≤ θ ≤ π .