Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.4 - Ex. 33

Encontre a área da região que está dentro de ambas as curvas.

r = 3 + 2   s e n   θ ,     r = 2

Passo 1

Olá, meu amigo. Vamos resolver essa atividade.

Precisamos aqui calcular a área da região que é comum as duas curvas polares.

Primeiro vamos esboçar as duas equações polares.

r = 3 + 2 sin ⁡ θ

é uma lima côncava (em magenta) e

  r   =   2  

também é um círculo centrado no polo com raio 2 (em turquesa).

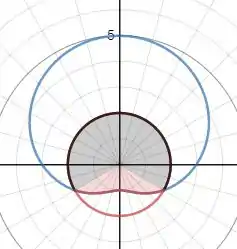
Vemos que existem dois pontos de interseção, um no terceiro quadrante e o outro no quarto quadrante. Podemos encontrá-los (pelo menos o valor de θ ) igualando as duas equações entre si.

Então vamos utilizar a fórmula de cálculo de área:

A = 1 2 ∫ b a r 2 d θ

E vamos calcular a área da região vermelha, e somar com a área da região preta, pois temos aqui á área que queremos é a junção dessas duas regiões.

Passo 2

Primeiramente vamos descobrir os ângulos θ onde as duas funções serão iguais, para isso vamos igualar o r de um com o r de outro:

3 + 2   s e n   θ = 2

s e n   θ = - 1 2

Com isso os valores de θ em radianos serão iguais a:

θ 1 = - π 6

θ 2 = - 5 6 π

Passo 3

Agora vamos plotar os dois gráficos dados na questão novamente.

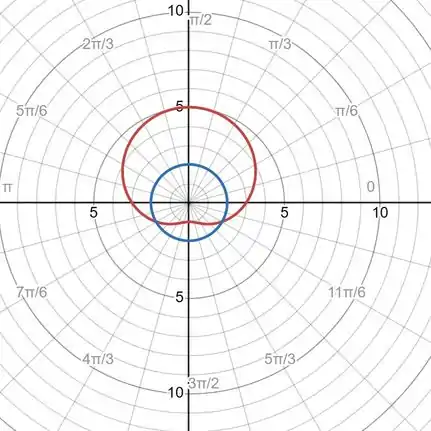
Onde a curva vermelha representa

r = 2

e a curva azul é

r = 3 + 2   s e n   θ

e por ela conseguimos ver que elas são simétricas na reta de x = 0 e também que antes da interseção com

θ = - π 6

a curva r = 2 apresenta um módulo maior que

r = 3 + 2   s e n   θ

e com valores maiores que esse (como θ = 0 por exemplo) nós temos que

r = 3 + 2   s e n   θ

apresenta um valor maior que r = 2 o que faz com que a área entre os dois seja igual a:

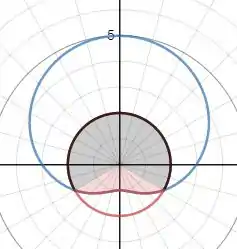
Onde a área vermelha é a área de

r = 3 + 2 sin ⁡ θ  

indo de - 5 π 6 até - π 6 e a área preta é a área de r = 2 indo de - π 6 até - 5 π 6 porém como elas são simétricas no eixo vertical nós vamos utilizar a seguinte fórmula para calcular essa área:

A = 2 ⋅ 1 2 ∫ - π 2 - π 6 3 + 2   s e n   θ 2 d θ + 1 2 ∫ - π 6 π 2 2 2 d θ  

Passo 4

Fazendo o produto notável do primeiro termo, e já realizando a integral do segundo termo:

A = ∫ - π / 2 - π / 6 9 + 12   s e n   θ + 4   s e n 2 θ d θ + 4 θ - π / 6 π / 2

Para fazer a integral de s e n 2 θ nós devemos saber duas relações trigonométricas tais como:

s e n 2 θ + cos 2 ⁡ θ = 1

cos 2 ⁡ θ - s e n 2 θ = cos ⁡ 2 θ

Logo:

s e n 2 θ = 1 - cos ⁡ 2 θ 2

Logo a integral será:

∫ s e n 2 θ = 1 2 θ - 1 4 sin ⁡ 2 θ

Substituindo na nossa integral temos:

A = ∫ - π 2 - π 6 ( 9 + 12 s e n   θ + 2 - 2 cos ⁡ 2 θ )   d θ + 4 π 2 + π 6

Agora resolvendo esse integral aí nós teremos:

A = 9 θ - 12 cos ⁡ θ + 2 θ - sin ⁡ 2 θ - π / 2 - π / 6 + 8 π 3

Agora aplicando o intervalo:

A = 11 - π 6 + π 2 - 12 cos ⁡ - π 6 + 12 cos ⁡ - π 2 - sin ⁡ ( - π 3 ) + sin ⁡ - π + 8 π 3

Realizando os cálculos:

A = 11 π 3 - 12 3 2 + 0 + 3 2 - 0 + 8 π 3

A = 19 π 3 - 11 3 2

Resposta

A = 19 π 3 - 11 3 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre os comprimentos das curvas nos Exercícios 25-30.29. x = 8 c o s t + 8 ts e nt ,y = 8s e nt - 8 t c o s t ,0 ≤ t ≤ π / 2
Encontre os comprimentos das curvas nos Exercícios 25-30.25. x = c o s t ,y = t + s e nt ,0 ≤ t ≤ π
Assumindo que as equações nos Exercícios 15-20 definem x e y implicitamente como funções deriváveis x = f ( t ) ,y = g ( t ) , encontre o coeficiente angular da curva x = f ( t ) ,y = g ( t ) no valor
Encontre os comprimentos das curvas nos Exercícios 25-30.27. x = t 2 / 2 ,y = ( 2 t + 1 ) 3 / 2 / 3 ,0 ≤ t ≤ 4
Encontre os comprimentos das curvas nos Exercícios 25-30.28. x = ( 2 t + 3 ) 3 / 2 / 3 ,y = t + t 2 / 2 ,0 ≤ t ≤ 3