Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.4 - Ex. 44
Use um gráfico para estimar os valores de para os quais as curvas e se interceptam. Então estime a área que está dentro de ambas as curvas.
Passo 1
Eaee, tudo bem?? Bom... o enunciado pede para a gente estimar, utilizando uma ferramenta matemática, os valores de onde as seguintes curvas se interceptam:
Depois que plotarmos elas, iremos estimar a área que está dentro de ambas as curvas.
Olha... vamos plotar logo para ficar melhor de entendermos a questão. Em azul está a curva e, em vermelho, a curva :
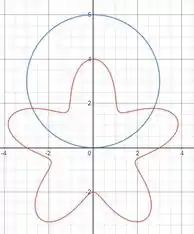
Queremos calcular essa área em verde:
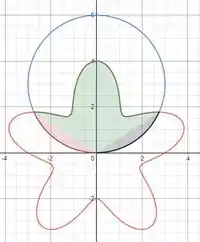
Para isso, a gente vai calcular essa área através da seguinte expressão:
Onde iremos descobrir os intervalos de integração através dos pontos de interseção entre as curvas.
Agora bora lá!! 😉
Passo 2
Bom... é difícil dizer em que ângulo ela intercepta hahahah.
Aqui é melhor usar outro que analisa essas duas funções em coordenadas cartesianas mesmo, veja:
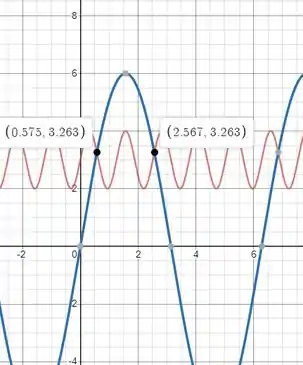
Onde temos os valores de ângulos em radianos iguais a:
Passo 3
A área entre os dois gráficos é a que está desenhada abaixo:
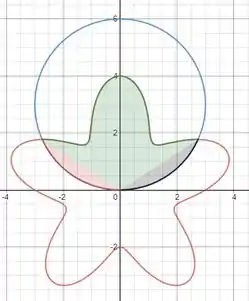
Onde as áreas vermelha e preta são as áreas de (curva azul) indo de até (área preta) e indo de até .
A área verde é a área de indo de até .
Isso pode ser visto pois entre esses dois ângulos a estrelinha fica abaixo do círculo e em outros o círculo que fica abaixo.
Porém elas são simétricas na reta vertical do plano cartesiano o que nos abre a possibilidade de escrever a fórmula da área da seguinte forma:
Passo 4
Para fazer a integral de temos que saber que:
Logo:
Substituindo isso na integral temos:
Agora só resolver esse monstrinho.
Essa contaralhada dá: