Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 8

Encontre a área da região sombreada:

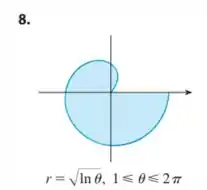
Passo 1

Olá, vamos resolver essa atividade. Aqui iremos calcular a área da figura:

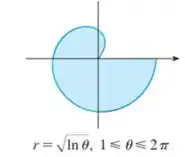
Temos em mão tanto o intervalo quanto a equação do raio da figura.

E para calcularmos a área em uma equação parametrizada em coordenadas polares, precisamos apenas aplicar a seguinte equação:

A = ∫ 1 2 π 1 2 r 2 d θ

A = ∫ 1 2 π 1 2 ln ⁡ θ 2 d θ

Passo 2

Primeiro vamos resolver a integral indefinida, depois substituímos os limites no resultado:

∫ 1 2 ln ⁡ θ 2 d θ = 1 2 ∫ ln ⁡ θ d θ

Podemos resolver por integração por partes, pois como temos uma função logarítmica aqui, uma substituição não irá funcionar.

∫ u d v = u ⋅ v - ∫ v d u

Chamamos u θ = ln ⁡ θ ⇒ u ' θ = 1 θ e v ' θ = 1 ⇒ v ( θ ) = θ , ficamos com:

1 2 ∫ ln ⁡ θ d θ = 1 2 θ ln ⁡ θ - ∫ 1 d θ

Resolvendo a última integral:

1 2 θ ln ⁡ θ - θ + c

Passo 3

Substituindo os limites 1 ≤ θ ≤ 2 π :

A = 1 2 θ ln ⁡ θ - θ + c 1 2 π

A = 1 2 2 π ln ⁡ 2 π - 2 π - 1 2 ln ⁡ 1 - 1

A = 1 2 2 π ln ⁡ 2 π - 2 π + 1

Que é aproximadamente:

A ≅ 3,13

E terminamos aqui nossa resolução!

Resposta

A ≅ 3,13

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Trace a curva e calcule a área delimitada por ela. r = 1 + 5s e n6 θ
Encontre a área da região que está dentro da primeira curva e fora da segunda curva: r = 2 + s e n θ r = 3 s e n θ
Encontre a área da região que é limitada pela curva dada e está localizada no setor especificado. r = c o s θ , 0 ≤ θ ≤ π 6
Encontre a área da região que é limitada pela curva dada e está localizada no setor especificado. r = 1 θ , π / 2 ≤ θ ≤ 2 π
Encontre a área da região que é limitada pela curva dada e está localizada no setor especificado.3. r = s e n θ + c o s θ , 0 ≤ θ ≤ π