Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 26
Encontre a área da região que está dentro da primeira curva e fora da segunda curva.
26. ,
Passo 1
A figura abaixo mostra o gráfico das duas regiões:
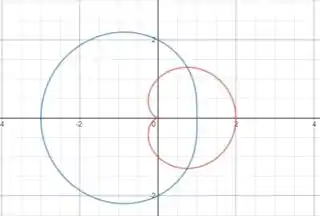
Precisamos encontrar a área da região que está dentro da curva vermelha e fora da curva azul, os pontos onde elas se intersecionam serão os limites de integração da equação da área:
Para encontrarmos esses pontos, vamos igualar as equações das duas curvas:
Como a região é simétrica em relação a ao eixo x, podemos integrar no intervalo e multiplicar a integral por dois. A equação da área então fica:
Onde e .
Passo 2
Primeiro vamos resolver a integral indefinida, e ao final substituímos os limites:
Expandindo os polinômios:
Somando os termos:
Integrando:
Passo 3
Substituindo os limites:
Resposta
Exercícios de Livros Relacionados
Calcule a área da superfície gerada pela rotação da curva dada em torno do eixo y .65. x = 3 t 2 , y = 2 t 3 ,0 ≤ t ≤ 5
Se o arco da curva no Exercício 50 girar em torno do eixo x , estime a área da superfície resultante usando a Regra de Simpson com n = 4 .
Trace a curva x = 2 cos θ - cos 2 θy = 2 s e nθ - s e n 2 θ Se essa curva girar em torno do eixo x , calcule a área da superfície resultante. (Use o gráfico para ajudar a encontrar o intervalo cor
Encontre a fórmula para a área da superfície gerada pela rotação da curva polar r = f θ , a ≤ θ ≤ b (onde f ' é contínua e 0 ≤ ab ≤ π ) , em torno da reta θ = π 2 . Calcule a área da superfície gerada
Encontre a área da região sombreada, onde r = θ .