Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.4 - Ex. 8
Encontre a área da região sombreada.
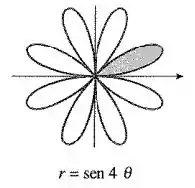
Passo 1
Queremos encontrar a área da região sobreada limitada pela curva
Para isso, vamos usar a expressão da área em coordenadas polares:
Mas para isso, temos que descobrir os limites de integração e para a região sombreada!
Temos que nessa região, completa um ciclo indo de , passando pelo seu valor máximo e depois retornando até . Isso significa que foi de até , isto é
Ou ainda
Portanto, os limites de integração são
Assim, substituindo os limites de integração e a curva na fórmula, temos
E respondendo essa integral nós teremos a nossa resposta!
Passo 2
Temos
Vamos fazer uma mudança de variáveis:
De forma que,
Assim,
Além disso, temos a identidade trigonométrica
De forma que a nossa integral fica
Fazendo a integração:
Aplicando os limites, chegamos em
Se quiséssemos a área da curva toda, bastaria multiplicar essa resposta por pois temos oito laços!