Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.2 - Ex. 55
(a) Use evidências numéricas e gráficas para fazer uma conjectura sobre o valor do limite
(b) A que distância de deverá estar para garantir que a função da parte (a) esteja a uma distância de de seu limite?
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu o seguinte limite:
Vamos chamar .
Primeiramente queremos estimar o valor do limite utilizando uma tabelinha relacionando e quando .
Para isso, vamos verificar os limites laterais para . Lembrando que o limite nesse ponto só existe se os limites laterais forem iguais (ou seja, se for contínua nesse ponto).
Em seguida, queremos saber a que distância de deverá estar para garantir que a função esteja a uma distância de de seu limite.
Agora bora aplicar!! 😉
Passo 2
Vamos elaborar uma tabelinha para o limite lateral esquerdo, ou seja, para:
Assim, selecionando alguns valores de , temos:
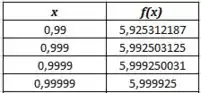
Agora, fazendo de forma análoga para o limite lateral direito
Temos a seguinte tabelinha:
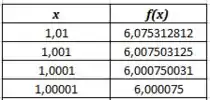
Perceba que ambos os limites convergem para , ou seja:
Passo 3
Utilizando uma software matemático, vamos verificar a função no ponto :
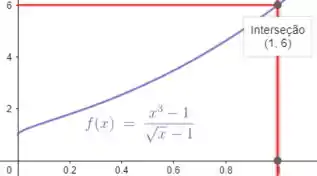
Logo, percebe-se que o limite analisado no passo 2 é verdadeiro.
Passo 4
Agora, queremos saber a que distância de deverá estar para garantir que a função esteja a uma distância de de seu limite.
Dado que o limite é , aplicando a distância de do limite, temos o seguinte intervalo:
Vamos marcar no gráfico os ponto para e :
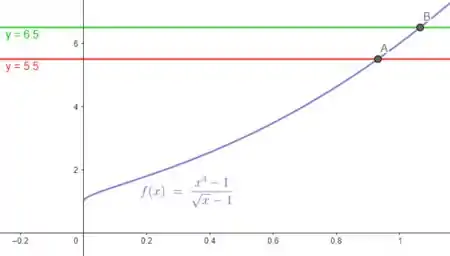
Dessa forma, vemos que os pontos de interseção foram:
E
Como queremos a distância que deverá estar , temos, para o ponto :
E, para o ponto :
Resposta
e