Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.6 - Ex. 37B
Estime o valor de usando uma tabela de valores para para conjecturar o valor do limite
Passo 1
Pronto para mais uma resolução meu amigo?
A gente vai calcular o limite dessa função, de um jeito mais manual.
Para resolver este item da questão, construiremos uma tabela de valores, onde será confrontado com os valores , seja
Iremos aqui diminuir o valor de cada vez mais, e assim poderemos analisar o limite da função para .
Passo 2
Vamos então construir a nossa tabela:
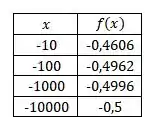
Por meio da análise da tabela podemos observar que quanto menor o valor de , se aproxima . Logo,
Resposta
Exercícios de Livros Relacionados
Ache o limite, se existir.underset(x - - oo)(lim) (4 x - 3)/(5 x^2 - x + 1)
Ache o limite, se existir.underset(x - + oo)(lim) ((8 x^3 + 7 x - 2)/(7 x^3 + 3 x^2 + 5 x))^2
Ache o limite, se existir.underset(t - + oo)(lim) (sqrt(t^2 + t) - sqrt(t^2 + 4))
Por comportamento final de uma função queremos indicar uma descrição do que acontece com seus valores quando x → ∞ e quando x → - ∞ .Descreva e compare o comportamento final das funções P x = 3 x 5 -
Calcule o limite, se existir.underset(h - 0)(lim) (sqrt(9 + h) - 3)/(h)