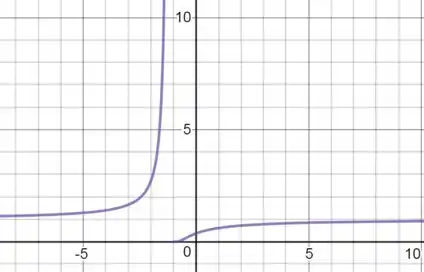
(a) Encontre as assíntotas vertical e horizontal.
(b) Encontre os intervalos nos quais a função é crescente ou decrescente.
(c) Encontre os valores máximos e mínimos locais.
(d) Encontre os intervalos de concavidade e os pontos de inflexão.
(e) Use a informação das partes (a)-(d) para esboçar o gráfico de .
Passo 1
Faala meus queridões! Bora fazer mais uma questão de gráfico? Isso cai bastante em prova, então vamos com cuidado aqui...
Nessa questão temos a seguinte função:
E o enunciado pede para a gente algumas coisas.
Primeiro queremos encontrar as assíntotas.
Uma assíntota vertical é aquela no qual a função tende para mais ou menos infinito. Para isso vamos procurar por pontos onde a função não seja definida, onde ela tenha uma descontinuidade.
Uma assíntota horizontal é um valor real que a função tende quando vai para menos ou mais infinito:
Ou
Queremos encontrar os intervalos em que ela é crescente ou decrescente. Para isso vamos derivar a função e fazer um estudo de sinais da derivada, pois quando a derivada é positiva a função é crescente
E quando a derivada é negativa, a função é decrescente.
Depois disso vamos encontrar os pontos de máximo e mínimo.
Para isso, vamos encontrar os pontos onde a derivada vale zero.
Ou pontos onde a derivada não exista:
Esses são pontos críticos da nossa função.
Para verificar se eles são pontos de máximo ou mínimo vamos olhar para o comportamento da derivada ao redor deles.
Se a derivada é positiva antes do ponto crítico e negativa depois do ponto crítico, então esse é um ponto de máximo.
Se a derivada é negativa antes do ponto crítico e positiva depois dele, então esse é um ponto de mínimo.
E por fim vamos olhar para os intervalos de concavidade e os pontos de inflexão.Para isso, vamos encontrar a segunda derivada da nossa função e fazer um estudo de sinais dela.
Quando a segunda derivada é positiva, a concavidade é para cima.
Quando a segunda derivada é negativa, a concavidade é para baixo.
E quando a segunda derivada é zero, temos um ponto de inflexão.
E por fim, vamos usar esses resultados e tentar traçar um gráfico da nossa função.
Passo 2
A assíntota vertical pode ser obtida nesse caso pelo limite de quando converge para o valor onde a função não está definida, o que neste caso é pois não existe divisão por zero.
Vamos olhar aqui para esse limite por ambos os lados.
E isso resulta em:
Já pelo outro lado, teremos:
O que já vai dar:
Portanto, quando tende a , a função tende a zero pela esquerda e tende a infinito positivo pela direita, e por isso, é uma assíntota vertical:
As assíntotas horizontais são os valores que converge quando tende aos infinitos:
E
Passo 3
Se
Então, para deriva-la, vamos aplicar uma regra da cadeia e uma regra do quociente:
Para crescente:
Aqui temos uma divisão de funções. O numerador nunca é negativo, pois temos uma exponencial que é sempre positiva. E o denominador nunca é negativo, pois temos uma potência de grau par.
Dessa forma, é crescente em todo o seu domínio.
Temos ainda que essa derivada não é definida em .
Passo 4
Se é crescente em todo o seu domínio, então não possui máximo nem mínimo local.
Passo 5
Se
Então, aplicando a regra do quociente, temos:
Derivando e aplicando a regra da cadeia quando necessário, temos:
Simplificando o que dá e colocando em evidência, temos:
Para com concavidade para cima:
Aqui, temos que todas as funções são positivas, com exceção do polinômio que está no numerador, dessa forma, será ele que irá dizer se a segunda derivada é positiva ou negativa, portanto:
Para com concavidade para baixo:
Assim, possui concavidade para cima em valores de no intervalo e concavidade para baixo em . Então, o ponto de inflexão é em .
Passo 6
Pelas informações obtidas:
(a)
(b) é crescente em todo o seu domínio.
(c) não possui máximo nem mínimo local.
(d) possui concavidade para cima em valores de no intervalo e concavidade para baixo em . Então, o ponto de inflexão é em .
Podemos traçar o seguinte gráfico:
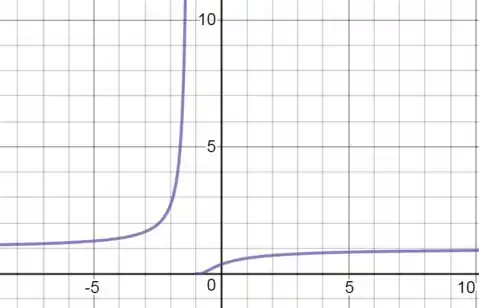
Resposta
(a)
(b) é crescente em todo o seu domínio.
(c) não possui máximo nem mínimo local.
(d) possui concavidade para cima em valores de no intervalo e concavidade para baixo em . Então, o ponto de inflexão é em .
(e)