Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 72
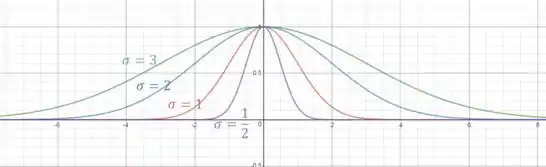
A família das curvas em forma de sino
Ocorre em probabilidade e estatística, nas quais ela é chamada função densidade normal. A constante é denominada média, e a constante positiva é conhecida como desvio padrão. Por simplicidade, mudamos a escala da função de forma a remover o fator e vamos analisar o caso especial onde . Logo, estudamos a função
(a) Encontre a assíntota, o valor máximo e os pontos de inflexão de .
(b) Que papel desempenha no formato da curva?
(c) Ilustre, fazendo o gráfico de quatro membros dessa família sobre a mesma tela.
Passo 1
Eaeee, belezinha? Bom... a questão nos dá uma gaussiana (ou curva normal) da seguinte forma:
Para facilitar nossa vida, a questão simplificou para a seguinte função:
Com isso, devemos calcular no item (a) a assíntota, o valor máximo e os pontos de inflexão de .
E precisamos lembrar que:
A assíntota vertical pode ser obtida nesse caso pelo limite de quando converge para o valor onde a função não está definida, o que neste caso não ocorre já que está definida para todo número real, então não há nenhuma assíntota vertical.
As assíntotas horizontais são os valores que converge quando tende aos infinitos:
Para encontrar o valor máximo dá função podemos usar o teste da primeira derivada. Assim:
No tesnte da Primeira primeira derivada lembraremos que a derivada de uma função é igual a inclinação da reta tangente ao gráfico da função. Assim, Se
Então a ideia é achar os pontos críticos fazendo a derivada igual a zero, e depois analisar o sinal da derivada em pontos antes e depois do ponto crítico.
E para encontra o ponto de inflexão, fazemos a derivada de segunda ordem ir a zero.
Assim:
Será um ponto de inflexão onde a função muda a direção de sua concavidade.
Depois, no item (b) devemos dizer qual é a função que desempenha nessa função e plotar um gráfico com a “família de sinos”. Para isso usaremos uma calculadora gráfica.
E aí? Bora lá??
Passo 2
Vamos começar a resolver o item (a), procurando os pontos críticos da função. Para isso vamos derivar a função:
Perceba que ela é uma função composta. Sendo assim, devemos usar a regra da cadeia. Fazendo:
Então:
Que ajustando se torna:
Invertendo o termo de expoente negativo, teremos:
E veja que para crescente:
Como a exponencial nunca é negativa, teremos:
Ou melhor:
E para decrescente:
Assim:
Ou melhor:
Então é crescente em e decrescente em . Como cresce ate e decresce a partir daí, temos um valor máximo em .
Passo 3
Agora vamos derivar novamente a função. Assim, se
Sua derivada serpa calculada usando a regra do quociente. Assim, fazemos:
E
sende
Com
E
Com
E a derivada será:
Organizando os sinais, teremos:
E colocando em evidência:
Simplificando o , temos:
Fazendo o mmc no numerador, teremos:
E dividindo as frações, teremos:
Prontinho, agora vamos analisar
Passo 4
Para com concavidade para cima:
Assim,
E olhando para o numerador:
ou
Para com concavidade para baixo:
E olhando para o numerador:
Assim, possui concavidade para cima em valores de no intervalo e e concavidade para baixo em .
Então, vemos que os pontos de inflexão são e .
Passo 5
Item b:
O papel que desempenha no formato da curva é onde ocorre o ponto de inflexão. Quando temos mudança de concavidade e, portanto, afinando ou alargando o formato do sino.
Passo 6
Item c:
De acordo com o que foi obtido, temos o gráfico:
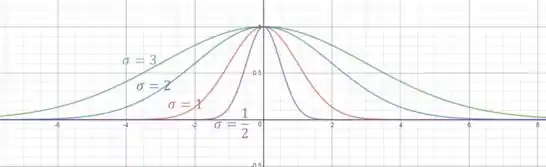
Resposta
(a)
Assíntotas:
Valor máximo em
Os pontos de inflexão são e .
(b) Afinando ou alargando o formato do sino.
(c)
