42) Em Physics: Calculus, de Eugene Hecht, ed., Pacific Grove, CA, Brooks/Cole, 2002, p. durante a dedução da fórmula para o período de um pêndulo de comprimento , o autor obtém a equação para a aceleração tangencial do peso do pêndulo. Ele então afirma: “para ângulos pequenos, o valor de em radianos é muito próximo do valor de ; eles diferem por menos do que até cerca de ”
(a) Verifique a aproximação linear em para a função seno:
(b) Use uma ferramenta gráfica para determinar os valores de para os quais e difiram por menos que . Então, verifique a afirmação de Hecht, convertendo de radianos para graus.
Passo 1
Oiie, bora resolver essa comigo
A aproximação linear é baseada no conceito de tangente a uma curva em um ponto específico. Se considerarmos um ponto em uma curva representada por uma função , a linha tangente a essa curva nesse ponto é uma aproximação linear da função nesse ponto.
A equação geral de uma linha reta é dada por onde é a inclinação da reta e é o intercepto no eixo y. Na aproximação linear, a inclinação é dada pela derivada da função em ou seja, O intercepto é determinado substituindo na equação da reta, ou seja,
Portanto, a equação da reta tangente (ou aproximação linear) à função em torno do ponto é dada por:
Essa equação da reta tangente é a aproximação linear da função em torno do ponto Essa aproximação é válida apenas para pequenos desvios de
Passo 2
Letra a:
Para obter a linearização uma função , devemos utilizar a aproximação da função em :
Para isso vamos derivar :
Então, em é:
Logo, a linearização está correta.
Passo 3
Letra b:
Queremos os valores para os quais o módulo do erro é menor que , ou seja:
Se chamarmos , então queremos os valores para os quais .
O gráfico de é:
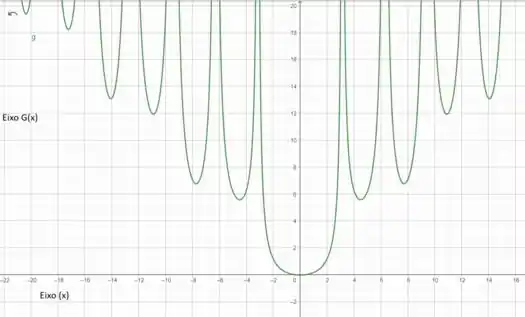
Passo 4
Como podemos ver, só é negativa para valores de bem próximos de (zero), mas diferentes de zero pois a função não está definida para (não existe divisão por 0).
Temos que quando ou , logo, o intervalo de que procuramos é:
Se o ângulo é de radianos, então ele corresponde a . Logo, a afirmação de Hecht é comprovada pois esse valor não ultrapassa .
Resposta
(a) A linearização está correta.
(b) A afirmação de Hecht é comprovada pois esse valor não ultrapassa .