(a) Encontre as assíntotas vertical e horizontal.
(b) Encontre os intervalos nos quais a função é crescente ou decrescente.
(c) Encontre os valores máximos e mínimos locais.
(d) Encontre os intervalos de concavidade e os pontos de inflexão.
(e) Use a informação das partes (a)-(d) para esboçar o gráfico de .
Passo 1
Oiee, bora resolver essa comigo:
Vamos analisar cada parte do enunciado e o que ela pede em relação à função
Para a letra (a), o enunciado pede as assíntotas Vertical e Horizontal:
- Assíntotas Verticais: São os valores de onde o denominador da função se anula. No caso de o denominador é .
Portanto, encontramos as assíntotas verticais onde ou seja,
- Assíntota Horizontal: É o valor para o qual a função tende quando se aproxima do infinito. Para quando tende ao infinito, a função se aproxima de
Então, é uma assíntota horizontal.
Para a letra (b), o enunciado pede os intervalos de Crescimento e Decrescimento:
- Para encontrar esses intervalos, precisamos examinar onde a função está aumentando (crescente) ou diminuindo (decrescente). Isso pode ser feito analisando os sinais da primeira derivada da função .
Já para a letra (c), o enunciado nos pede os valores Máximos e Mínimos Locais:
- Esses valores ocorrem onde a derivada da função muda de positiva para negativa (máximo local) ou de negativa para positiva (mínimo local). Podemos encontrar esses pontos verificando as mudanças de sinal na primeira derivada de .
Para a letra (d), o enunciado nos pede os intervalos de Concavidade e Pontos de Inflexão:
- A concavidade da função muda onde a segunda derivada muda de sinal. Pontos de inflexão ocorrem onde a concavidade muda.
E por fim na letra (e), ele pede que esbocemos o Gráfico de :
- Com todas essas informações, podemos esboçar o gráfico da função, considerando as assíntotas, os intervalos de crescimento e decrescimento, os valores máximos e mínimos locais, os intervalos de concavidade e os pontos de inflexão.
Isso nos dá uma boa compreensão do comportamento geral da função e como ela se parece.
Passo 2
Item a:
A assíntota vertical pode ser obtida nesse caso pelo limite de quando converge para o valor onde o denominador é zero que é ou .
Então:
E
As assíntotas horizontais são os valores que converge quando tende aos infinitos:
E
Passo 3
Para encontrar os intervalos de crescimento e decrescimento da função da letra (b)
Precisamos analisar os sinais da primeira derivada, .
Começamos encontrando a primeira derivada da função:
Para simplificar a diferenciação, podemos reescrever a função como:
Passo 4
Usando a regra do quociente e a regra do produto, podemos derivar a função:
Simplificando, obtemos:
Agora, para determinar os intervalos de crescimento e decrescimento, precisamos analisar os sinais de
- Quando a função está crescendo.
- Quando , a função está decrescendo.
Passo 5
Para encontrar os intervalos de crescimento, precisamos analisar onde a primeira derivada é positiva.
A primeira derivada
É positiva quando o numerador é positivo e o denominador é positivo, exceto onde , pois nesse caso a derivada não está definida.
Passo 6
Vamos encontrar onde
Para
- para todos os valores de neste intervalo.
- O numerador é negativo.
- Portanto, \) é negativo para
Para
- para todos os valores de neste intervalo.
- O numerador é positivo.
- Portanto, é positivo para
Para
- para todos os valores de neste intervalo.
- O numerador é positivo.
- Portanto, é positivo para
Portanto, os intervalos de crescimento de são
Passo 7
Para resolver a letra (c), que pede para encontrar os valores máximos e mínimos locais da função
Precisamos examinar onde a derivada muda de positiva para negativa (máximo local) ou de negativa para positiva (mínimo local).
Vamos começar encontrando os pontos críticos, que são os valores de onde a primeira derivada se anula ou não está definida.
Já calculamos a primeira derivada anteriormente:
A primeira derivada não está definida quando
Isso ocorre quando ou seja,
Então, temos dois pontos críticos:
Agora, para determinar se esses pontos são máximos ou mínimos locais, podemos usar o teste da derivada segunda.
Passo 8
Vamos encontrar a segunda derivada
Podemos simplificar o cálculo da segunda derivada utilizando a regra do quociente e do produto:
Agora, vamos avaliar a segunda derivada nos pontos críticos
Para
Passo 9
Como o denominador é zero, precisamos usar um outro método para determinar o tipo de ponto crítico em
Vamos usar o teste da primeira derivada.
Vimos anteriormente que para é positiva, e para é positiva também. Isso indica que em temos um mínimo local.
Para
Da mesma forma, como o denominador é zero, precisamos usar outro método para determinar o tipo de ponto crítico em
Vamos usar o teste da primeira derivada novamente. Vimos anteriormente que para é negativa. Isso indica que em temos um máximo local.
Então, os valores máximos e mínimos locais da função ocorrem em:
- Máximo local em .
- Mínimo local em .
Passo 10
Para a letra d, vamos verificar a concavidade e os pontos de inflexão para a função
Derivada Primeira:
Derivada Segunda:
Concavidade:
Para determinar a concavidade, analisamos o sinal de
- quando e ou seja,
- quando e , ou seja, ou
Passo 11
Os pontos de inflexão ocorrem onde muda de sinal. Neste caso, os pontos são pontos onde a concavidade muda, mas:
- Para não está definida, pois o denominador se torna zero.
Portanto, a resposta correta é:
- Nos intervalos possui concavidade para baixo.
- No intervalo possui concavidade para cima.
- Os valores não são pontos de inflexão reais, pois a função não está definida nesses pontos.
Passo 12
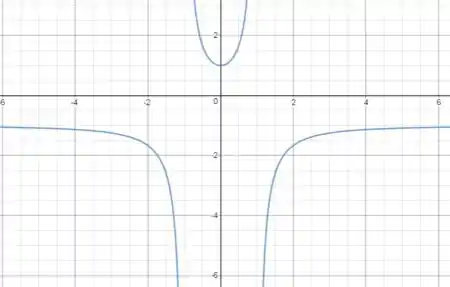
Item e:
Pelas informações obtidas temos o gráfico:
Resposta
Vide o passo a passo.