Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.4 - Ex. 110
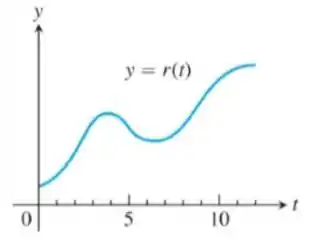
O gráfico a seguir mostra a receita mensal da Widget Corporation nos últimos 12 anos. Durante aproximadamente quais intervalos de tempo a receita marginal foi crescente? E decrescente?
Passo 1
A receita marginal é crescente quando a derivada segunda é positiva, ou seja, a concavidade da função é para cima. Vai ser nos intervalos: e .
Agora, receita marginal é decrescente quando a derivada segunda é negativa, ou seja, a concavidade da função é para baixo. Isso acontece nos intervalos: e .
Só isso! 😊
Resposta
e
e .
Exercícios de Livros Relacionados
35. (a) Use o método de Newton para encontrar os números críticos da função f x = x 6 - x 4 + 3 x 3 - 2 x com precisão de três casas decimais. (b) Encontre o valor mínimo absoluto de f com precisão de
24. Use o método de Newton para encontrar todas as raízes da equação com precisão de oito casas decimais. Comece fazendo um gráfico para encontrar a aproximação inicial. cos x 2 - x = x 4
24. Use o método de Newton para encontrar todas as raízes da equação com precisão de oito casas decimais. Comece fazendo um gráfico para encontrar a aproximação inicial x 5 - 3 x 4 + x 3 - x 2 - x + 6
Encontre as assíntotas verticais e horizontais.Encontre os intervalos nos quais a função é crescente ou decrescente.Encontre os valores máximos e mínimos locais.Encontre os intervalos de concavidade e
Encontre os intervalos em que a função é crescente ou decrescente.Encontre os valores máximo e mínimo locais. Encontre os intervalos de concavidade e pontos de inflexão. Use as informações de a)-c) pa