Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.6 - Ex. 44a
Para encontre cada um dos seguintes limites:
Passo 1
Falaaa... tudo bem?? Nessa questão vamos encontrar o limite:
Primeiro vamos lembrar que qualquer número (exceto infinito) divido por infinito é igual a , de forma geral é:
Passo 2
Beleza, agora a gente separa o limite em dois, porque a gente pode, e porque facilita nossa vida:
Passo 3
Então, a gente já pode aplicar aquilo que eu falei no passo 1 da divisão de qualquer número por infinito, fica assim:
Passo 4
Show de bola, a gente deve dar uma lembradinha no gráfico da função do logaritmo natural:
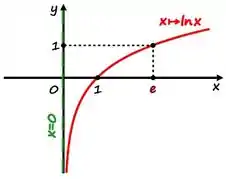
Tá vendo que quando aumenta a função também cresce infinitamente? Então:
Passo 5
Calma tá acabando, agora é só a gente aplicar o limite:
Resposta
Exercícios de Livros Relacionados
Ache o limiteunderset(y - + oo)(lim) (2 y^2 - 3 y)/(y + 1)
Ache o limiteunderset(w - - oo)(lim) (sqrt(w^2 - 2 w + 3))/(w + 5)
Ache o limiteunderset(x - + oo)(lim) (1 + 5 x)/(2 - 3 x)
Ache o limite:underset(x - + oo)(lim) (x^2 + 5)/(x^3)
Ache o limiteunderset(x - - oo)(lim) (5 x^3 - 12 x + 7)/(4 x^2 - 1)