Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.6 - Ex. 43a
Para encontre cada um dos seguintes limites:
(i)
(ii)
(iii)
Passo 1
Bom galera, primeiro vamos começar observando o gráfico do logaritmo natural:
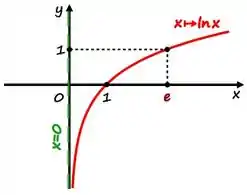
Assim a gente sabe alguns limites tipo:
Passo 2
Beleza, agora a gente aplica no denominador de cada limite que temos que calcular:
(i)
(ii)
(iii)
Passo 3
Agora, a gente já pode aplicar cada um dos limites, tendo cuidado com os sinais, bem assim:
(i)
(ii)
(iii)
Resposta
(i)
(ii)
(iii)
Exercícios de Livros Relacionados
Demonstre cada afirmação usando a definição ϵ , δ de limite. lim x → 2 x 2 - 4 x + 5 = 1
Demonstre cada afirmação usando a definição ϵ , δ de limite. lim x → a c = c
Demonstre cada afirmação usando a definição ϵ , δ de limite. lim x → 0 x 2 = 0
Verifique, usando argumento geométricos, que a maior escolha possível para o δ para que se possa mostrar que lim x → 3 x 2 = 9 é δ = 9 + ϵ - 3 .
Demonstre cada afirmação usando a definição ϵ , δ de limite. lim x → 0 | x | = 0