Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.6 - Ex. 42
Encontre o centro de massa do sólido com a dada função de densidade .
que é o tetraedro delimitado pelos planos , .
Passo 1
Fala, galera! Tudo joia?
Nesse exercício, iremos analisar o sólido que é delimitado pelos planos:
com função densidade
A questão pede para encontrarmos o centro de massa desse sólido . O centro de massa está localizando no ponto , onde:
Onde é a massa do sólido dada por:
E são os momentos em relação aos planos, que são calculados por:
Percebe que também falta acharmos os limites de integração das nossas integrais triplas. Como a função que estamos integrando está em relação a 3 variáveis , temos que achar os limites de integração para cada uma delas. Para achar esses limites vamos achar a projeção do nosso sólido no plano e seu comportamento em relação ao eixo .
Em resumo, precisaremos achar a massa e cada um dos momentos , para assim acharmos a localização do centro de massa.
Vem!
Passo 2
Vamos começar achando nossos limites de integração:
A imagem a seguir ilustra a região de interesse descrita no enunciado:
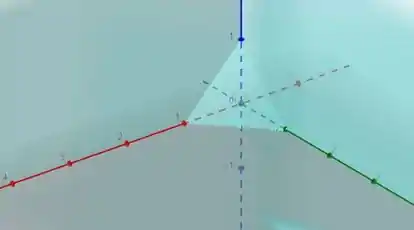
tetraedro delimitado pelos planos , com função densidade .
Lembrando que estamos interessados somente na parte acima do plano , devido ao limite .
- Para achar os limites de : fazemos e assim a gente entende qual é a interseção do tetraedro em :
- Para achar os limites de :
- Para achar os limites de : temos que . Isolando:
Então, temos que:
O valor mínimo de é zero devido ao limite do plano .
Sabemos que começa em zero pelo plano . Para saber onde vai, fazemos , assim estaremos olhando só para o plano :
Isolando :
Então:
Temos:
Então:
Passo 3
Agora que temos nossos limites de integração definidos, podemos começar a calcular as integrais triplas. Vamos começar pela integral da massa :
Dessa forma, podemos escrever a integral como:
Iremos calcular a integral como uma integral iterada, dessa forma, começando por , tratando as demais variáveis como constantes:
Aplicando os limites de integração em :
Simplificando a expressão, temos:
Passo 4
Agora iremos integrar em função de , tratando como constante:
Aplicando os limites em :
E, simplificando a expressão, temos:
Agora iremos integrar em relação a :
Aplicando nossos limites de integração:
Dessa forma, a massa é:
Passo 5
Para calcular a posição do centro de massa do sólido, iremos calcular os momentos de massa do solido com relação aos 3 eixos. Começaremos com relação ao eixo :
Dessa forma, podemos escrever a integral como:
Iremos calcular a integral como uma integral iterada, dessa forma, começando por e tratando as demais incógnitas como se fossem constantes:
Aplicando os limites em :
Simplificando a expressão, temos:
Agora iremos integrar em função de , tratando como constante:
Aplicando os limites em :
E, simplificando a expressão, temos:
Agora iremos integrar em relação a :
Aplicando os limites:
Dessa forma, temos:
Passo 6
Vamos calcular nosso momento :
Dessa forma, podemos escrever a integral como:
Iremos calcular a integral como uma integral iterada, dessa forma, começando por , tratando como constante:
Aplicando os limites de integração:
Simplificando a expressão, temos:
Agora iremos integrar em função de , tratando como constante:
Aplicando os limites em :
E, simplificando a expressão, temos:
Agora iremos integrar em relação a :
Aplicando os intervalos de integração:
Dessa forma, temos:
Passo 7
Calma que falta mais um momento para calcularmos. É o último! Agora com relação ao eixo :
Dessa forma, podemos escrever a integral como:
Iremos calcular a integral como uma integral iterada, dessa forma, começando por , que é a integral mais interna, olhando como constante:
Aplicando nossos limites de integração:
Simplificando a expressão, temos:
Agora iremos integrar em função de :
E aplicar nossos intervalos de integração:
E, simplificando a expressão, temos:
Agora iremos integrar em relação a :
Aplicando os intervalos:
Dessa forma, temos:
Passo 8
Chegamos ao final! Com os valores de massa e momentos em mãos, basta substituirmos.
Com isso, o centro de massa é dado por:
Sendo assim: