Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.6 - Ex. 39

Encontre o centro de massa do sólido E com a dada função de densidade ρ .

E é o sólido acima do plano x y e abaixo do paraboloide z = 1 - x 2 - y 2 ; ρ x , y , z = 3

Passo 1

E aí, pessoal! Firmeza?

Nesse exercício, iremos analisar o sólido E que fica acima do plano x y e abaixo do paraboloide:

z = 1 - x 2 - y 2

com função densidade

ρ x , y , z = 3

A questão pede para encontrarmos o centro de massa desse sólido E . O centro de massa está localizando no ponto ( x , - y , - z - ) , onde:

x - = M y z m

y - = M x z m

z - = M x y m

Onde m é a massa do sólido dada por:

m = ∫ ∫ ∫ ρ x , y , z d V

Então, para o nosso caso precisaremos calcular a integral tripla da função densidade ρ dada no enunciado:

m = ∫ ∫ ∫ 3   d V

E M são os momentos em relação aos planos, que são calculados por:

M y z = ∭ E x   ρ x , y , z d V

M x z = ∭ E y   ρ x , y , z d V

M x y = ∭ E z ρ x , y , z d V

Percebe que também falta acharmos os limites de integração das nossas integrais triplas. Como a função que estamos integrando está em relação a 3 variáveis x , y , z , temos que achar os limites de integração para cada uma delas. Para achar esses limites vamos achar a projeção do nosso sólido no plano x y e da equação do paraboloide.

Em resumo, precisaremos achar a massa m e cada um dos momentos M , para assim acharmos a localização do centro de massa.

Bora lá!

Passo 2

Vamos começar encontrando os limites de integração da nossa região E . A imagem a seguir ilustra a região de interesse descrita no enunciado:

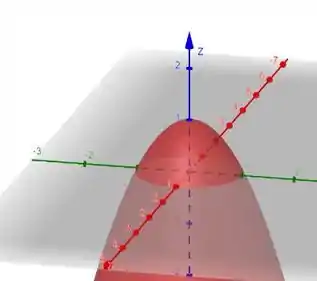
Lembrando que estamos interessados somente na parte acima do plano x y , como o enunciado pede.

Através da imagem podemos perceber que a projeção de E no plano x y é um círculo com raio variando de 0 a 1.

x 2 + y 2 = 1

Sendo assim, iremos converter as coordenadas x e y para o sistema de coordenadas polares após integrar em z , já que a região do círculo, que a gente descreve mais fácil em coordenadas polares estão no plano x y . Para z temos os limites 0 e o próprio paraboloide, então mantemos em coordenadas retangulares mesmo:

∫ ∫ ∫ 0 1 - x 2 - y 2 3 d z d A

Iremos calcular a integral como uma integral iterada, dessa forma, começando por z . Resolvendo a integral acima e aplicando os limites de integração:

∫ ∫ 3 z z = 0 z = 1 - x 2 - y 2 d A = ∫ ∫ [ 3 1 - x 2 - y 2 - 0 ] d A

Simplificando a expressão, temos:

∫ ∫ 3 ( 1 - x 2 - y 2 ) d A

Passo 3

∫ ∫ 3 ( 1 - x 2 - y 2 ) d A

Agora sim estamos no plano x y , pois faltam as integrais de x e y e podemos finalmente usar nossas coordenadas polares, já que nesse plano temos a região circular.

Agora iremos passar o sistema de coordenadas cartesiano para polar fazendo

x = r c o s   θ

  y = r s e n θ

Dessa forma, temos:

3 ∫ 0 2 π ∫ 0 1 ( 1 - r 2 cos 2 ⁡ θ - r 2 s e n 2   θ )   r d r d θ

Isolando r 2 :

3 ∫ 0 2 π ∫ 0 1 ( 1 - r 2 ( cos 2 ⁡ θ + s e n 2   θ ) )   r d r d θ

Lançando mão da relação fundamental s e n 2   x + cos 2 ⁡ x = 1 . E, substituindo, obtemos:

3 ∫ 0 2 π ∫ 0 1 ( 1 - r 2 )   r d r d θ

Iremos separar a integral em r e θ e resolver simultaneamente, sendo assim, temos:

3 ∫ 0 2 π d θ ∫ 0 1 r - r 3 d r = 3 θ 0 2 π 1 2 r 2 - 1 4 r 4 0 1

Aplicando os limites de integração:

3 2 π - 0 1 2 1 2 - 1 4 1 4 - 0

Dessa forma, a massa é:

m = 3 2 π

Passo 4

Para calcular a posição do centro de massa do sólido, iremos calcular os momentos de massa do solido com relação aos 3 eixos. Começaremos com o momento em relação ao eixo x . Para essas integrais de M vamos ter os mesmos limites de integração que achamos no passo acima:

M y z = ∫ ∫ ��� x ρ x , y , z d V = ∫ ∫ ∫ 0 1 - x 2 - y 2 3 x d z d A

Resolvendo a integral e calculando os limites de integração:

∫ ∫ 3 x z z = 0 z = 1 - x 2 - y 2 d A = ∫ ∫ [ 3 x 1 - x 2 - y 2 - 0 ] d A

Simplificando:

∫ ∫ 3 x 1 - x 2 - y 2 d A

Agora iremos passar o sistema de coordenadas cartesiano para polar fazendo x = r c o s   θ ,   y = r s e n θ . Dessa forma, temos:

3 ∫ 0 2 π ∫ 0 1 r c o s θ   1 - r 2 cos 2 ⁡ θ - r 2 s e n 2   θ   r d r d θ

Isolando r 2 :

3 ∫ 0 2 π ∫ 0 1 r c o s θ   1 - r 2 ( cos 2 ⁡ θ + s e n 2   θ )   r d r d θ

Lançando mão da relação fundamental s e n 2   x + cos 2 ⁡ x = 1 . E, substituindo, obtemos:

3 ∫ 0 2 π ∫ 0 1 r c o s θ   ( 1 - r 2 )   r d r d θ

Iremos separar a integral em r e θ e resolver simultaneamente, sendo assim, temos:

3 ∫ 0 2 π c o s θ d θ ∫ 0 1 r 2 - r 4 d r = 3 sen ⁡ θ 0 2 π 1 3 r 3 - 1 5 r 5 0 1

Aplicando os limites de integração:

3 0 - 0 1 3 1 3 - 1 5 1 5 - 0

Dessa forma, temos:

M y z = 0

Passo 5

Agora, para o eixo y :

M x z = ∫ ∫ ∫ y ρ x , y , z d V = ∫ ∫ ∫ 0 1 - x 2 - y 2 3 y d z d A

∫ ∫ 3 y z z = 0 z = 1 - x 2 - y 2 d A = ∫ ∫ [ 3 y 1 - x 2 - y 2 - 0 ] d A

∫ ∫ 3 y ( 1 - x 2 - y 2 ) d A

Agora iremos passar o sistema de coordenadas cartesiano para polar fazendo x = r c o s   θ ,   y = r s e n θ . Dessa forma, temos:

3 ∫ 0 2 π ∫ 0 1 ( r s e n θ ) ( 1 - r 2 cos 2 ⁡ θ - r 2 s e n 2   θ )   r d r d θ

Isolando r 2 :

3 ∫ 0 2 π ∫ 0 1 ( r s e n θ ) ( 1 - r 2 ( cos 2 ⁡ θ + s e n 2   θ ) )   r d r d θ

Lançando mão da relação fundamental s e n 2   x + cos 2 ⁡ x = 1 . E, substituindo, obtemos:

3 ∫ 0 2 π ∫ 0 1 r s e n θ ( 1 - r 2 )   r d r d θ

Iremos separar a integral em r e θ e resolver simultaneamente, sendo assim, temos:

3 ∫ 0 2 π s e n θ d θ ∫ 0 1 r 2 - r 4 d r = 3 - cos ⁡ θ 0 2 π 1 3 r 3 - 1 5 r 5 0 1

3 [ - 1 - - 1 ] 1 3 1 3 - 1 5 1 5 - 0

Dessa forma, temos:

M x z = 0

Passo 6

Agora, para o eixo z :

M x y = ∫ ∫ ∫ z ρ x , y , z d V = ∫ ∫ ∫ 0 1 - x 2 - y 2 3 z d z d A

Resolvendo e aplicando os limites de integração:

∫ ∫ 3 2 z 2 z = 0 z = 1 - x 2 - y 2 d A = ∫ ∫ 3 2 1 - x 2 - y 2 2 - 0 2 d A

Ficamos com:

∫ ∫ 3 2 1 - x 2 - y 2 2 d A

Agora iremos passar o sistema de coordenadas cartesiano para polar fazendo x = r c o s   θ ,   y = r s e n θ e d A = r   d r   d θ . Dessa forma, temos:

3 2 ∫ 0 2 π ∫ 0 1 1 - r 2 cos 2 ⁡ θ - r 2 s e n 2   θ 2   r d r d θ

Isolando r 2 :

3 2 ∫ 0 2 π ∫ 0 1 1 - r 2 ( cos 2 ⁡ θ + s e n 2   θ ) 2   r d r d θ

Lançando mão da relação fundamental s e n 2   x + cos 2 ⁡ x = 1 . E, substituindo, obtemos:

3 2 ∫ 0 2 π ∫ 0 1 ( 1 - 2 r 2 + r 4 )   r d r d θ

Iremos separar a integral em r e θ e resolver simultaneamente, sendo assim, temos:

3 2 ∫ 0 2 π d θ ∫ 0 1 r - 2 r 3 + r 5 d r = 3 2 θ 0 2 π 1 2 r 2 - 1 2 r 4 + 1 6 r 6 0 1

Aplicando os limites de integração:

3 2 [ 2 π - 0 ] 1 2 1 2 - 1 2 1 4 + 1 6 1 6 - 0

Dessa forma, temos:

M x y = 1 2 π

Passo 7

Com isso, o centro de massa é dado por:

x - , y - , z - = M y z m , M x z m , M x y m

Substituímos os valores que achamos ao decorrer da resolução:

x - , y - , z - = 0 3 2 π , 0 3 2 π , 1 2 π 3 2 π

Sendo assim:

x - , y - , z - = 0,0 , 1 3

Resposta

m = 3 2 π

x - , y - , z - = 0,0 , 1 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a massa e o centro de massa do sólido dado E com função densidade dada ρ . E é o cubo dado por 0 ≤ x ≤ a , 0 ≤ y ≤ a , 0 ≤ z ≤ a ; ρ x , y , z = x 2 + y 2 + z 2
Determine a massa e o centro de massa do sólido dado E com função densidade dada ρ . E é o tetraedro limitado pelos planos x = 0 ,y = 0 ,z = 0 ,x + y + z = 1 ρ x , y , z = y
Determine a massa e o centro de massa do sólido dado E com função densidade dada ρ . E é limitado pelo cilindro parabolóico z = 1 - y 2 e pelos planos x + z = 1 , x = 0 e z = 0 ; ρ x , y , z = 4
Utilize coordenadas cilíndricas.Determine a massa da bola B dada por x 2 + y 2 + z 2 ≤ a 2 se a densidade em qualquer ponto for proporcional à sua distância do eixo z .
Utilize coordenadas cilíndricas.Determine a massa e o centro de massa do sólido S delimitado pelo paraboloide z = 4 x 2 + 4 y 2 e pelo plano z = a( a0 ) , se S tem densidade constante K .