Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.1 - Ex. 17
Encontre o comprimento exato da curva.
Passo 1
Opa! Bora resolver esse problema?! O enunciado pede pra a gente calcular o comprimento exato da seguinte curva:
O comprimento da curva é dado por:
Vamos derivar a função então:
Para isso usamos a regra da cadeia:
Aplicamos na fórmula agora:
Passo 2
Vamos resolver essa integral:
Mas:
Então:
Podemos usar frações parciais pra reescrever:
Fazendo a divisão de polinômio:
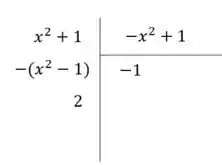
Então:
No denominador temos uma diferença de quadrados, então:
Podemos usar frações parciais pra fazer:
Então:
Passo 3
Chegamos em:
Vamos resolver cada integral separadamente:
Usando integral por substituição:
De modo similar temos:
Voltando pra integral original com os limites de integração:
Vamos aplicar os limites de interação agora:
Lembrando que:
Então temos:
Resposta
Exercícios de Livros Relacionados
Calcule a área do conjunto de todos os pontos ( θ , ρ ) tais que θ ²≤ ρ ≤ θ ²
Calcule a área de interseção da região limitada pelas curvas: ρ = s e n θ ρ = c o s ( θ )
Sejam F1 e F2 dois pontos distintos do plano e seja K a metadeda distância de F1 a F2. O lugar geométrico do Ponto P do plano tais que PF1 * PF2 = K² se chama lemniscata de focos F1 e F2.Tomando-se F1
Calcule a área de interseção da região limitada pelas curvas: ρ = cos θ ρ =√ s e n ( θ ) ρ ≥ 0
Calcule a área de interseção da região limitada pelas curvas: ρ = s e n θ ρ = 1 - cos θ