Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.7 - Ex. 5
Calcule a área do conjunto de todos os pontos (tais que
Passo 1
Primieramente, vamos separar nossas duas situações:
Podemos ver que o único intervalo que satisfaz as 2 inequações é [0,1]. Logo, os pontos de interseção são e
Passo 2
Vamos então olhar o gráfico para poder entender melhor o comportamento das funções.
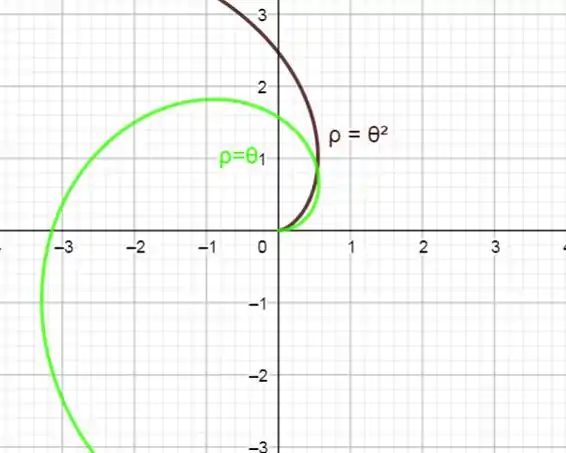
Agora fica mais fácil vizualizar que a área entre as curvas é a área da curva preta menos a área da curva verde, ambas de 0 até 1.
Passo 3
Sabemos que a fórmula para a área em coordenadas polares é:
0,5
Aplicando os limites de integração:
4d
Resolvendo a integral simples:
4d =
Resposta
A área do conjunto de pontos vale
Exercícios de Livros Relacionados
Ache a massa total e o centro de massa.20. Uma barra tem 10 cm e medida da densidade linear em um ponto é uma função linear da medida da distancia ao centro da barra. A densidade linear em cada extrem
Achar a massa total e o centro de massa.19. A medida da densidade linear em qualquer ponto de uma barra com 6 m varia diretamente com a distância do ponto a um ponto externo na reta suporte da barra e
Ache a massa total e o centro de massa18. O comprimento da barra é 10 m e a medida da densidade linear em um ponto é uma função linear da medida da distância do ponto ao extremo esquerdo da barra. A d
27. Uma barra tem 6 m de comprimento e sua massa é de 24 kg. Se a medida da densidade linear em qualquer ponto da barra varia diretamente com o quadrado da distância do ponto a um extrmo, ache o maior
26. A massa total de uma barra com L m de comprimento é M kg e a medida da densidade linear num ponto a x m do extremo esquerdo é proporcional a medida da distância do ponto ao extremo direito. Mostre