Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.7 - Ex. 7b

Escreva, em coordenadas polares, a equação da elipse x 2 a 2 + y 2 b 2 = 1 , tomando como pólo o foco F   =   ( c , 0 ) ,   c > 0 , e como eixo polar a semi-reta F A onde A = ( a , 0 ) ,   a > 0 . Faça e = c a e ρ = a - e c .

Passo 1

Primeiramente, vamos fazer o MMC:

b 2 x 2 a 2 b 2 + a 2 y 2 a 2 b 2 =   1

b 2 x 2 +   a 2 y 2 =   a 2 b 2

Agora vamso desenhar o triângulo retângulo:

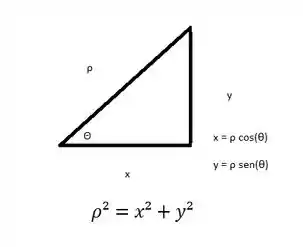
Logo, na primeira parcela:

b 2 ρ ² c o s 2 θ + a 2 ρ ² s e n 2 θ = a 2 b 2

ρ ² = a 2 b 2 b 2 c o s 2 θ + a 2 s e n 2 θ

Passo 2

O próximo passo é substituir os dados do problema:

e = c a e ρ = a - e c

Logo,

ρ = a - c 2 a

Substituindo na equação que encontramos no passo 1

ρ ² = a 2 b 2 b 2 c o s 2 θ + a 2 s e n 2 θ → a - c 2 a 2 =   a 2 b 2 b 2 c o s 2 θ + a 2 s e n 2 θ

Ajeitando,

a 2 + c 2 a 2 2 =   a 2 b 2 b 2 c o s 2 θ + a 2 s e n 2 θ

Com isso ficamos com,

a 4   + 2 a 2 c 2 +   c 4 a 4   = a 2 b 2 b 2 c o s 2 θ + a 2 s e n 2 θ

Resposta

A equação da elipse, em coordenadas polares, é :

a 4   + 2 a 2 c 2 +   c 4 a 4   =   = a 2 b 2 b 2 c o s 2 θ + a 2 s e n 2 θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache o comprimento da curva 9 y 2 = 4 1 + x 2 3 no primeiro quadrante, do ponto onde x = 0 ao ponto onde x = 2 2 .
Ache o comprimento da curva 9 y 2 = x 2 2 x + 3 no segundo quadrante, do ponto x = - 1 ao ponto onde x = 0 .
Ache o comprimento da curva 9 y 2 = x x - 3 2 no primeiro quadrante, do ponto onde x = 1 ao ponto onde x = 3 .
Ache o comprimento do arco de curva x a 2 3 + y b 2 3 = 1 no primeiro quadrante, do ponto x = 1 8 a ao ponto onde x = a .
Ache o comprimento do arco da curva y = ln x entre x = 1 e x = 3 .