Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 8
Encontre as dimensões de um retângulo com área de cujo perímetro seja o menor possível.
Passo 1
Fala aí, galerinha! 😊
Bom, essa questão pede pra gente encontrar as dimensões de um retângulo com área de cujo perímetro seja o menor possível.
😐
Então a ideia aqui é a seguinte:
Vamos modelar esse retângulo como sendo:
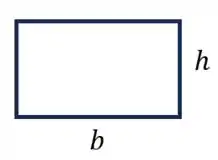
Assim sua área será:
E seu perímetro
E como queremos o descobrir as dimensões que fazem com que o perímetro seja o menor possível, vamos usar a informação da área para escrever o perímetro em função de uma única variável.
Assim, podemos usar a derivada do perímetro em função dessa variável para nos ajudar a encontrar seus valor mínimo. Já que:
Será um ponto crítico que pode ser de máximo ou mínimo.
Vem que vou te ajudar a ver tudo isso acontecendo.
Bora lá! 😉
Passo 2
usando a informação da área, podemos isolar uma das variáveis:
Assim,
Agora podemos substituir na expressão do perímetro. E ficaremos com:
Maravlinha.
Passo 3
Para encontrar o mínimo, basta derivarmos e igualar a zero.
Como:
Teremos que usar a regra do quociente, já que essa função é formada pela divisão entre duas outras funções. Assim, lembrando que:
Então
Assim, nossa derivada será:
E ajustando, temos:
Ou melhor
Passo 4
Agora vamos procurar seu valor mínimo igualando a derivada a zero. Assim:
Então:
Como o denominador nunca pode ser igual a zero, basta olharmos para o numerador, então:
E isolando , teremos:
Show.
agora nos resta encontrar .
Teremos:
E racionalizando, ficamos com:
As dimensões são e
E aí! entendeu tudo? Responde Aí!
Resposta
As dimensões são e