Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.7 - Ex. 24
Encontre as dimensões do retângulo de maior área que tem sua base sobre o eixoe seus dois outros vértices acima do eixo e sobre a parábola .
Passo 1
Fala aí, tudo belezinha?
Bom, essa questão pede pra gente encontrar as dimensões do retângulo de maior área que tem sua base sobre o eixoe seus dois outros vértices acima do eixo e sobre a parábola
E para isso, precisamos entender que como esse retângulo é construído graficamente, e depois procurar suas dimensões ideais para que tenhamos a maior área possível.
Então a ideia aqui será a seguinte: traçaremos a parábola
e localizaremos a construção do retângulo para encontrar uma expressão para sua área.
Depois faremos a maximização dessa área através do seu valor máximo que pode ser encontrado fazendo a derivada igual a zero.
Assim acharemos suas dimensões ideais.
Vem que te mostro tudinho.
Passo 2
Vamos começar traçando a parábola
E localizando o retângulo pedido. Assim, teremos:
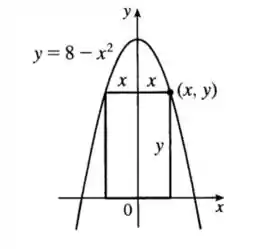
Observe que a largura desse retângulo vale , e sua altura, , assim, temos uma expressão para a área, dada por:
.
O já nos é dado pela fórmula da parábola e vale , com isso, podemos fazer a substituição na fórmula da área:
E multiplicando o na distributiva, teremos:
Maravilha, essa é nossa expressão para a área do retângulo dependendo apenas do valor de .
Passo 3
Agora, dependendo de apenas uma variável, , será possível fazer a maximização derivando e igualando a zero, para encontramos as dimensões máximas.
Sendo:
Sua derivada será calculada usando a regra do expoente em cada um dos termos, assim:
Como queremos maximizar esta área, faremos:
Assim:
Isolando , teremos:
Maravilha, já temos o valor ideal de , agora vamos procura .
Substituindo em :
E essas são as dimensões do retângulo de maior área que obedece ao que o enunciado pediu.
Resposta
Dimensões do retângulo:
Largura =
Altura =