Encontre o domínio e esboce o gráfico da função:

Bom pessoal , primeiramente temos que olhar e pensar: que tipo de restrição pode ter no domínio da função? De cara, vemos que o numerador da expressão configura uma função do segundo grau, então com ela ta tudo ok, visto que é uma função simples e sem nenhum tipo de complicação. No denominador a gente tem um restrição, a de que ele não pode ser zero, ou seja:

Ajeitando a expressão, temos que a única restrição de domínio da função será:

Ou seja, o domínio da nossa função será todos os números reais menos o número . Podemos escrever que o domínio da função vai ser todos os reais, desde que seja diferente de . A gente pode escrever isso em linguagem matemática, ficando assim:

Tranquilo até aqui? 😊

Para achar o gráfico da função, a gente vai ter que mexer um pouquinho na forma dela. Na parte de cima, podemos escrever como . Isso daí é uma diferença de quadrados, certo? É o resultado de um produto notável do tipo (produto da soma pela diferença). Esses produtos notáveis tem que estar embalados na cabeça, não esquece disso, fechou? Agora a gente vai mexer na nossa função:

Beleeeeeza! Temos o termo no numerador e no denominador, então a gente pode cortar um com o outro. Mas não vai esquecer: essa função não existe no ponto de jeito nenhum! E a gente só pode cancelar os termos se respeitar isso, tranquilo? Olha só como vai ficar nossa expressão:

Essa daí é uma função do primeiro grau, que é representada por uma reta. Quando , teremos e quando , teremos . Pronto, agora temos dois pontos da nossa reta e podemos desenhá-la! Dá uma checada em como vai ficar o gráfico:

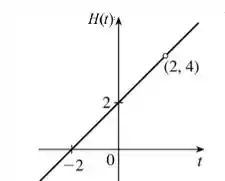
No ponto temos uma bolinha vazia porque a função não existe quando devido a restrição do domínio que a gente achou beeem no início, tranquilo? Pronto! Essa questão já era! ;)

Entendeu tudo? Responde Aí! 😉