Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.1 - Ex. 44
- Use uma calculadora gráfica ou computador para fazer o gráfico da função na janela retangular por
- Usando o gráfico da parte (a) para estimar a inclinação, faça um esboço, à mão, do gráfico de (veja o Exemplo 1 da Seção 2.8).
- Calcule e use essa expressão, como uma ferramenta gráfica, para fazer o gráfico de . Compare com seu esboço da parte (b).
Passo 1
- Esboçando o gráfico:
- Vemos no gráfico em (a) que há pontos extremos em e em, logo, a derivada nesses pontos é zero. A inclinação é negativa ( é negativo) em . As inclinações são positivas ( é positivo) em e em .
- Calculando:
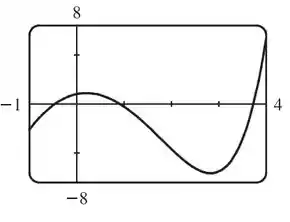
Passo 2
Esboço do gráfico:
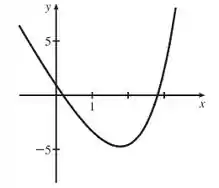
Passo 3
Esboço do gráfico:
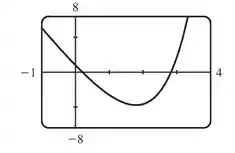
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Use o roteiro desta seção para esboçar a curva. y = x - ln x
Na teoria da relatividade, a massa de uma partícula é m = m 0 1 - v 2 c 2 Em que m 0 é a massa de repouso da partícula, m é a massa quando a partícula se move com velocidade v em relação ao observador
Use o roteiro desta seção para esboçar a curva. y = ln x x 2
Use o roteiro desta seção para esboçar a curva. y = x e - x 2
Use o roteiro desta seção para esboçar a curva. y = e x x